题目内容
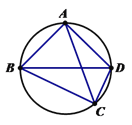
【题目】如图,点C为△ABD外接圆上的一点(点C不在![]() 上,且不与点B,D重合),且∠ACB=∠ABD=45°,若BC=8,CD=4,则AC的长为( )
上,且不与点B,D重合),且∠ACB=∠ABD=45°,若BC=8,CD=4,则AC的长为( )
A. 8.5 B. ![]() C.
C. 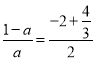 D.
D. ![]()
【答案】D
【解析】在CD延长线上截取DE=BC,连接EA,只需要证明△EAF是等腰直角三角形即可得出结论;
解:在CD的延长线上截取DE=BC,连接EA,
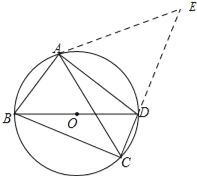
∵∠ABD=∠ADB,∴AB=AD,
∵∠ADE+∠ADC=180°,
∠ABC+∠ADC=180°,
∴∠ABC=∠ADE,
在△ABC与△ADE中,
AB=AD,∠ABC=∠ADE,BC=DE,
∴△ABC≌△ADE(SAS),
∴∠BAC=∠DAE,
∴∠BAC+∠CAD=∠DAE+∠CAD,
∴∠BAD=∠CAE=90°,
∵![]() =
=![]() ,
,
∴∠ACD=∠ABD=45°,
∴△CAE是等腰直角三角形,
∴![]() AC=CE,
AC=CE,
∴![]() AC=CD+DE=CD+BC;
AC=CD+DE=CD+BC;
∴AC=![]() .
.
“点睛”本题考查圆的综合问题,涉及圆周角定理,等腰三角形的性质,全等三角形的性质与判定等知识,综合程度较高,解决本题的关键就是构造等腰直角三角形.

【题目】某公司生产某种商品每件成本为20元,这种商品在未来40天内的日销售量y(件)与时间x(天)的关系如下表:
时间x(天) | 1 | 3 | 6 | 10 | ... |
日销售量y(件) | 94 | 90 | 84 | 76 | ... |
未来40天内,前20天每天的价格m(元/件)与时间x(天)的函数关系式为![]() (1≤x≤20),后20天每天的价格为30元/件(21≤x≤40).
(1≤x≤20),后20天每天的价格为30元/件(21≤x≤40).
(1)分析上表中的数据,用所学过的一次函数、二次函数、反比例函数的知识确定一个满足这些数据的y(件)与x(天)之间的函数关系式.
(2)当1≤x≤20时,设日销售利润为W元,求出W与x的函数关系式.
(3)在未来40天中,哪一天的日销售利润最大,最大日销售利润是多少?

