题目内容
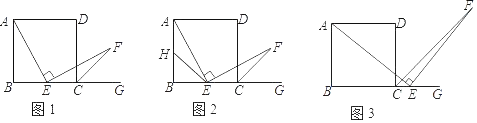
【题目】如图1,四边形ABCD是正方形,点E是边BC的中点,∠AEF=90°,且EF交正方形ABCD的外角∠DCG的平分线CF于点F.
(1)如图2,取AB的中点H,连接HE,求证:AE=EF.
(2)如图3,若点E是BC的延长线上(除C点外)的任意一点,其他条件不变结论“AE=EF”仍然成立吗?如果正确,写出证明过程:如果不正确,请说明理由.
【答案】(1)见解析;(2)成立,见解析.
【解析】
(1)取AB的中点H,连接EH,根据已知及正方形的性质利用ASA判定△AHE≌△ECF,从而得到AE=EF;
(2)成立,延长BA到M,使AM=CE,根据已知及正方形的性质利用ASA判定△AHE≌△ECF,从而得到AE=EF;
(1)证明:取AB的中点H,连接EH;如图1所示

∵四边形ABCD是正方形,AE⊥EF;
∴∠1+∠AEB=90°,∠2+∠AEB=90°
∴∠1=∠2,
∵BH=BE,∠BHE=45°,且∠FCG=45°,
∴∠AHE=∠ECF=135°,AH=CE,
在△AHE和△ECF中,
 ,
,
∴△AHE≌△ECF(ASA),
∴AE=EF;
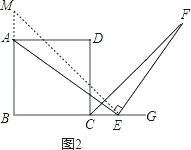
(2)解:AE=EF成立,
理由如下:如图2,延长BA到M,使AM=CE,
∵∠AEF=90°,
∴∠FEG+∠AEB=90°.
∵∠BAE+∠AEB=90°,
∴∠BAE=∠FEG,
∴∠MAE=∠CEF.
∵AB=BC,
∴AB+AM=BC+CE,
即BM=BE.
∴∠M=45°,
∴∠M=∠FCE.
在△AME与△ECF中,
 ,
,
∴△AME≌△ECF(ASA),
∴AE=EF.

 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案【题目】列一元一次方程解应用题:
某水果店计划购进![]() .
.![]() 两种水果,下表是
两种水果,下表是![]() .
.![]() 这两种水果的进货价格:
这两种水果的进货价格:
水果品种 |
|
|
进货价格(元 |
|
|
(1)若该水果店要花费![]() 元同时购进两种水果共
元同时购进两种水果共![]() ,则购进
,则购进![]() .
.![]() 两种水果各为多少
两种水果各为多少![]() ?
?
(2)若水果店将![]() 种水果的售价定为
种水果的售价定为![]() 元
元![]() ,要使购进的这批水果在完全售出后达到
,要使购进的这批水果在完全售出后达到![]() 的利润率,
的利润率,![]() 种水果的售价应该定为多少?
种水果的售价应该定为多少?