题目内容
【题目】已知正方形![]() 内接于
内接于![]() ,点
,点![]() 为
为![]() 上一点,连接
上一点,连接![]() 、
、![]() 、
、![]() .
.
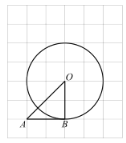
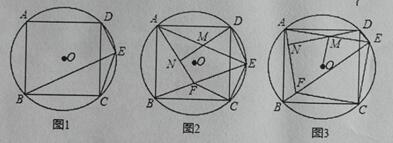
(1)如图1,求证:∠DEC+∠BEC= 180°;
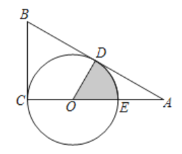
(2)如图2,过点C作CF⊥CE交BE于点F,连接AF, M为AE的中点,连接DM并延长交AF于点N,求证: DN⊥AF;
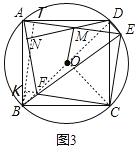
(3)如图3,在(2) 的条件下,连接OM,若AB=10,![]() 求OM的长.
求OM的长.
【答案】(1)证明过程见解析;(2)证明过程见解析;(3)![]() ;
;
【解析】
(1)连接BD,OC,得出∠BEC=45°,由圆周角定理可得出结论
(2)延长ED至G,使ED=DG,连接AG,证明△BFC≌△DEC,可得出BF=DE,证明△ABF≌△ADG,则∠BAF=∠DAC,证明DM∥AG,得出∠DNF=∠FAG=90°,则可得出结论;
(3)连接BD,OC,过点B作BK⊥CF交CF的延长线于点K,过点B作BT⊥AE于点T,设DE=x,则BE=7x,得出BD=5![]() x,求出x=2,求出BK=KF=
x,求出x=2,求出BK=KF=![]() ,由tan∠BCF=tan∠DCE=
,由tan∠BCF=tan∠DCE=![]() ,求出CF,可求出TB=7
,求出CF,可求出TB=7![]() ,AM=4
,AM=4![]() ,则可求出OM的长.
,则可求出OM的长.
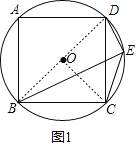
解:(1)证明:连接BD,OC,
∵四边形ABCD为正方形,
∴∠A=90°,BC= CD,
∴BD为⊙O的直径,即∠DEB=90°,
∵OB= OD,
∴OC⊥BD,即∠BOC= 90°,
∴∠BEC=![]() ∠ BOC=45°,
∠ BOC=45°,
∴∠DEC+∠BEC=∠DEB+∠BEC+∠BEC= 180°.
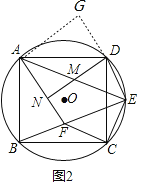
(2)证明:如图,延长ED至G,使ED=DG,连接AG,
∵CE⊥CF,∴∠ECF=90°,
∵∠CEF=45°,
∴∠CEF=∠CFE=45°,
∴CE= CF,
∵∠BCD=∠ECF=90°,
∴∠BCF=∠DCE,
∵BC=CD,
∴△BFC≌ODEC (SAS),即BF=DE ,
∵DE=DG,
∴BF=DG,
∵四边形ABED为圆O的内接四边形,
∴∠ABE+∠ADE= 180°,
∴∠ADE+∠ADG=180°,
∴∠ABE=∠ADG,
∵AB=AD,
∴△ABF≌OADG (SAS), 即∠BAF=∠DAG,
∵∠BAF+∠FAD=∠BAD=90°,
∴∠DAG+∠FAD=90°,即∠FAG= 90°.
∵M为AE的中点,
∴DM为△AEG的中位线,即DM// AG,
∴∠DNF=∠FAG=90°,即DN⊥AF.
(3)解:如图,连接BD,OC,过B作BK⊥CF的延长线于点K,
过点B作BT⊥AE于T,
由(1)知![]() ,则
,则![]() ,
,
由(1)知BD为⊙O的直径,
在![]() 中,
中,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
设DE=x,则BE=7x,
在![]() 中,
中,![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,即
,即![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
由(2)知![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,即
,即![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∵![]() 为
为![]() 的中点,∴
的中点,∴![]() ,
,
在![]() 中,
中,![]() .
.

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案