题目内容
【题目】热爱学习的小明同学在网上搜索到下面的文字材料:
在x轴上有两个点它们的坐标分别为![]() 和
和![]() .则这两个点所成的线段的长为
.则这两个点所成的线段的长为![]() ;同样,若在y轴上的两点坐标分别为(0,b)和(0,d),则这两个点所成的线段的长为|b-d|.如图1,在直角坐标系中的任意两点P1,P2,其坐标分别为(a,b)和(c,d),分别过这两个点作两坐标轴的平行线,构成一个直角三角形,其中直角边P1Q=|a-c|,P2Q=|b-d|,利用勾股定理可得,线段P1 P2的长为
;同样,若在y轴上的两点坐标分别为(0,b)和(0,d),则这两个点所成的线段的长为|b-d|.如图1,在直角坐标系中的任意两点P1,P2,其坐标分别为(a,b)和(c,d),分别过这两个点作两坐标轴的平行线,构成一个直角三角形,其中直角边P1Q=|a-c|,P2Q=|b-d|,利用勾股定理可得,线段P1 P2的长为![]() .
.

根据上面材料,回答下面的问题:
(1)在平面直角坐标系中,已知![]() ,
,![]() ,则线段AB的长为_____;
,则线段AB的长为_____;
(2)若点C在y轴上,点D的坐标是![]() ,且
,且![]() ,则点C的坐标是_____;
,则点C的坐标是_____;
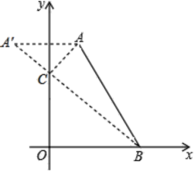
(3)如图2,在直角坐标系中,点A,B的坐标分别为![]() 和
和![]() ,点C是y轴上的一个动点,且A,B,C三点不在同一条直线上,求△ABC周长的最小值.
,点C是y轴上的一个动点,且A,B,C三点不在同一条直线上,求△ABC周长的最小值.
【答案】(1)6;(2)C的坐标为![]() 或
或![]() ;(3)
;(3)![]() 的周长的最小值为
的周长的最小值为![]() .
.
【解析】
(1)、(2)根据线段长度计算方法计算即可;
(3)找到点A关于y轴的对称点A′(-1,4),连接A′B交y轴于点C,此时△ABC周长的最小,即可求解.
(1)![]() .
.
因为![]() ,
,![]() 的横坐标相同,也可以直接用|a-c|求:|-1-5|=|-6|=6,
的横坐标相同,也可以直接用|a-c|求:|-1-5|=|-6|=6,
故答案为:6;
(2)设C点坐标为![]() ,
,
则在Rt△OCD中,![]() ,
,
解得![]() .
.
所以C的坐标为![]() 或
或![]() .
.
(3)设A点关于y轴的对称点为A′,则点A′的坐标为![]() ,当C点为A′B与y轴的交点时,
,当C点为A′B与y轴的交点时,![]() 的周长最小,因为AC= A′C,所以
的周长最小,因为AC= A′C,所以![]() 的周长
的周长![]() .
.
![]() .
.
![]() .
.
所以![]() 的周长的最小值为
的周长的最小值为![]() .
.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目







