题目内容
现有1240吨钢材,880吨水泥,准备用一列挂有A、B两种不同规格车厢的货车运往一城市的建筑工地。该货车有40节车厢,如果使用A型车厢每节费用为6000元,如果使用B型车厢每节费用为8000元。
小题1:设运送这批钢材和水泥的总费用为y万元,这列货车挂A型车厢x节,请写出y与x之间的函数关系式。
小题2:如果每节A型车厢最多可装钢材35吨和水泥15吨,每节B型车厢最多可装钢材25吨和水泥35吨,装货时按此要求安排A、B两种车厢的节数,那么共有哪几种安排车厢的方案?
小题3:在上述方案中,哪个方案运费最少?最少运费为多少?
小题1:设运送这批钢材和水泥的总费用为y万元,这列货车挂A型车厢x节,请写出y与x之间的函数关系式。
小题2:如果每节A型车厢最多可装钢材35吨和水泥15吨,每节B型车厢最多可装钢材25吨和水泥35吨,装货时按此要求安排A、B两种车厢的节数,那么共有哪几种安排车厢的方案?
小题3:在上述方案中,哪个方案运费最少?最少运费为多少?
小题1:y=-0.2x+32
小题2:方案:A24节 B16节, A25节 B15节 , A26节 B14节
小题3:当A26节 B14节时 最少运费为26.8万元
(1)y=-0.2x+32
(2)设A型车厢x节。则B型车厢(40-x)节
35x+25(40-x)≧1240
15x+35(40-x)≧880
解得:24≦x≦26
方案:A24节 B16节, A25节 B15节 , A26节 B14节
(3)当A24节 B16节时,运费=24×6000+16×8000=272000元;
当A25节 B15节时,运费=25×6000+15×8000=270000元;
当A26节 B14节时,运费=26×6000+14×8000=268000元.
故当A26节 B14节时 最少运费为26.8万元
(2)设A型车厢x节。则B型车厢(40-x)节
35x+25(40-x)≧1240
15x+35(40-x)≧880
解得:24≦x≦26
方案:A24节 B16节, A25节 B15节 , A26节 B14节
(3)当A24节 B16节时,运费=24×6000+16×8000=272000元;
当A25节 B15节时,运费=25×6000+15×8000=270000元;
当A26节 B14节时,运费=26×6000+14×8000=268000元.
故当A26节 B14节时 最少运费为26.8万元

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
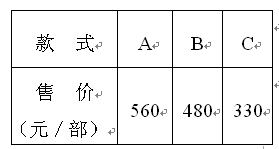
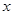 元,两项优惠共
元,两项优惠共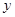 元,请写出
元,请写出

 ,C种票张数为
,C种票张数为 .
.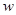 元,求出
元,求出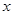 时,
时,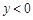 ;
;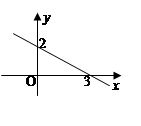
 与
与 轴交于点A,与
轴交于点A,与 轴交于点B.
轴交于点B.
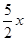 ,则自变量的取值范围为( )
,则自变量的取值范围为( )