题目内容
下列命题:
①若a+b+c=0,则b2-4ac<0;
②若b=2a+3c,则一元二次方程ax2+bx+c=0有两个不相等的实数根;
③若b2-4ac>0,则二次函数y=ax2+bc+c的图象与坐标轴的公共点的个数是2或3;
④若b>a+c,则一元二次方程ax2+bx+c=0有两个不相等的实数根.
其中正确的是
①若a+b+c=0,则b2-4ac<0;
②若b=2a+3c,则一元二次方程ax2+bx+c=0有两个不相等的实数根;
③若b2-4ac>0,则二次函数y=ax2+bc+c的图象与坐标轴的公共点的个数是2或3;
④若b>a+c,则一元二次方程ax2+bx+c=0有两个不相等的实数根.
其中正确的是
| A.②④ | B.①③ | C.②③ | D.③④ |
C
试题分析:解:①∵a+b+c=0,
∴b=-a-c,
∴b2-4ac=(-a-c)2-4ac=a2+2ac+c2-4ac=a2-2ac+c2=(a-c)2≥0,故错误;
②∵b=2a+3c,
∴b2-4ac=(2a+3c)2-4ac=4a2+12ac+9c2-4ac=4a2+8ac+9c2=4(a+c)2+5c2>0,
∴一元二次方程ax2+bx+c=0有两个不相等的实数根,故正确;
③∵b2-4ac>0,
∴抛物线与x轴有两个不同的交点,
∴二次函数y=ax2+bx+c的图象与坐标轴的公共点的个数是3或2,故正确;
④∵b>a+c,那么设b=2,a=-4,c=-2,
∴b2-4ac=4-32<0,
∴一元二次方程ax2+bx+c=0没有实数根,故错误.
点评:本题难度较低,主要考查学生学生对抛物线及根的判别式应用知识点的掌握。此题主要利用了二次函数y=ax2+bx+c的图象与x轴交点的个数的判断.

练习册系列答案
相关题目
 的根是 .
的根是 . ;
; 
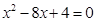 的两个根分别是a和b,则a+b=_______.
的两个根分别是a和b,则a+b=_______.
 的解为 .
的解为 .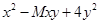 是一个完全平方式,那么
是一个完全平方式,那么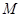 的值是( )
的值是( ) ,则x= .
,则x= .