题目内容
【题目】如图,已知一块四边形草地ABCD,其中∠A=45°,∠B=∠D=90°,AB=20m,CD=10m,求这块草地的面积. 
【答案】解:分别延长AD,BC交于点E.如图所示, 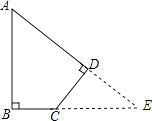
∵∠A=45°,∠B=∠D=90°,
∴∠DCE=∠DEB=∠A=45°,
∴AB=BE,CD=DE,
∵AB=20,CD=10,
∴BE=20,DE=10,
∵S△ABE= ![]() ABBE=200,S△CDE=
ABBE=200,S△CDE= ![]() CDDE=50,
CDDE=50,
∴四边形ABCD的面积=S△ABE﹣S△CDE=200﹣50=150m2 .
即这块草地的面积为:150m2
【解析】分别延长AD,BC交于点E,所求四边形ABCD的面积=S△ABE﹣S△CED . 由∠A=45°,∠B=∠D=90°,可得△ABE和△CDE都是等腰直角三角形,然后求出△ABE和△CDE的面积即可求解.
【考点精析】利用等腰直角三角形对题目进行判断即可得到答案,需要熟知等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目