题目内容
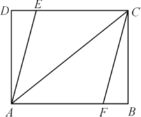
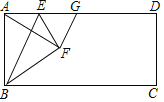
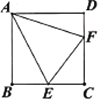
【题目】如图,正方形ABCD边长为6,E是BC的中点,连接AE,以AE为边在正方形内部作∠EAF=45°,边![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,则下列说法中:①
,则下列说法中:①![]() ;②
;②![]() ;③tan∠AFE=3;④
;③tan∠AFE=3;④![]() .正确的有( )
.正确的有( )
A.①②③B.②④C.①④D.②③④
【答案】D
【解析】
延长CB到G,使BG=DF,连接AG,证明△ABG≌△ADF,即可证得AG=AF,∠DAF=∠BAG,再证明△AEG≌△AEF,根据全等三角形的对应边相等即可得出结论.
证明:延长CB到G,使BG=DF,连接AG.如图所示:

∵四边形ABCD是正方形,
∴AB=AD,∠ABE=∠D=90°,
∴∠ABG=90°=∠D,
∵△ABG和△ADF中,
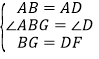
∴△ABG≌△ADF(SAS),
∴AG=AF,∠1=∠2,
又∵∠EAF=45°,∠DAB=90°,
∴∠2+∠3=45°,
∴∠1+∠3=45°,
∴∠GAE=∠EAF=45°.
在△AEG和△AEF中,
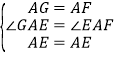
∴△AEG≌△AEF(SAS),
∴GE=EF,
∵GE=BG+BE,DF=BG,
∴EF=DF+BF,故②正确,
∵BE=EC=3,AB=6,
![]() ,
,
∴∠3≠30°,故①错误,
设DF=x,则EF=x+3,
在Rt△EFC中,∵EF2=CF2+EC2,
∴(x+3)2=32+(6-x)2,
∴x=2,
∴DF=BG=2,
![]() ,故③正确,
,故③正确,
![]() ,故④正确.
,故④正确.
故选:D.

练习册系列答案
相关题目