题目内容
如果从-2、1、3、4 四个数中任取一个数作为 a，从-2、l、4三个数中任取一个数作为 b，将取出的a和b两个数代入二次函数y=ax2-4x+b中，那么该二次函数的顶点在x轴上的概率为分析：二次函数的顶点在x轴上，则△=b2-4ac=0，所以（-4）×（-4）-4ab=0，即ab=4，利用列树状图或列表法，求得a与b的乘积，乘积为4即可，进而求得概率值即可．
解答：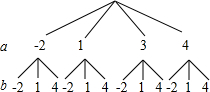
解：列树状图如图所示，共有12种结果，每种结果出现的可能性相同．
ab=4的结果共有3个，
故P=
=
．
故答案为：
．
解：列树状图如图所示，共有12种结果，每种结果出现的可能性相同．ab=4的结果共有3个，
故P=
| 3 |
| 12 |
| 1 |
| 4 |
故答案为：
| 1 |
| 4 |
点评：本题是二次函数与统计初步中的综合题型，要熟悉二次函数的性质，并会根据条件确定出符合条件的a与b的组合．会用列举法求出事件的概率．
练习册系列答案
提分百分百检测卷系列答案
宝贝计划期末冲刺夺100分系列答案
能考试全能100分系列答案
相关题目
康乐公司在A、B两地分别有同型号的机器17台和15台，现要运往甲地18台，乙地14台．从A、B两地运往甲、乙两地的费用如下表：
（1）如果从A地运往甲地x台，求完成以上调运所需总费用y（元）与x（台）的函数关系式；
（2）若康乐公司请你设计一种最佳调运方案，使总的费用最少，该公司完成以上调运方案至少需要多少费用？为什么？
| 甲地（元/台） | 乙地（元/台） | |
| A地 | 600 | 500 |
| B地 | 400 | 800 |
（2）若康乐公司请你设计一种最佳调运方案，使总的费用最少，该公司完成以上调运方案至少需要多少费用？为什么？
如图，一只蚂蚁从原点O出发，它先向右爬了2个单位长度到达点A，再向右爬3个单位长度到达点B，然后向左爬9个单位长度到达点C．