题目内容
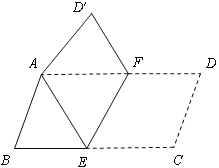
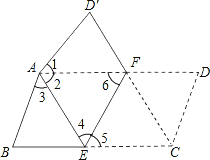
【题目】将平行四边形纸片![]() 按如图方式折叠,使点
按如图方式折叠,使点![]() 与
与![]() 重合,点
重合,点![]() 落到
落到![]() 处,折痕为
处,折痕为![]() .
.
(1)求证:![]() ;
;
(2)连结![]() ,判断四边形
,判断四边形![]() 是什么特殊四边形?证明你的结论.
是什么特殊四边形?证明你的结论.
【答案】(1)证明见解析;(2)四边形AECF是菱形.证明见解析.
【解析】
试题分析:(1)根据平行四边形的性质及折叠的性质我们可以得到∠B=∠D′,AB=AD′,∠1=∠3,从而利用ASA判定△ABE≌△AD′F;
(2)四边形AECF是菱形,我们可以运用菱形的判定,有一组邻边相等的平行四边形是菱形来进行验证.
试题解析:(1)由折叠可知:∠D=∠D′,CD=AD′,
∠C=∠D′AE.
∵四边形ABCD是平行四边形,
∴∠B=∠D,AB=CD,∠C=∠BAD.
∴∠B=∠D′,AB=AD′,∠D′AE=∠BAD,
即∠1+∠2=∠2+∠3.
∴∠1=∠3.
在△ABE和△AD′F中
∵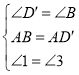
∴△ABE≌△AD′F(ASA).
(2)四边形AECF是菱形.
证明:由折叠可知:AE=EC,∠4=∠5.
∵四边形ABCD是平行四边形,
∴AD∥BC.
∴∠5=∠6.
∴∠4=∠6.
∴AF=AE.
∵AE=EC,
∴AF=EC.
又∵AF∥EC,
∴四边形AECF是平行四边形.
又∵AF=AE,
∴平行四边形AECF是菱形.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
【题目】深圳天虹某商场从厂家批发电视机进行零售,批发价格与零售价格如下表:
电视机型号 | 甲 | 乙 |
批发价(元/台) | 1500 | 2500 |
零售价(元/台) | 2025 | 3640 |
若商场购进甲、乙两种型号的电视机共50台,用去9万元.
(1)求商场购进甲、乙型号的电视机各多少台?
(2)迎“元旦”商场决定进行优惠促销:以零售价的七五折销售乙种型号电视机,两种电视机销售完毕,商场共获利8.5%,求甲种型号电视机打几折销售?