题目内容
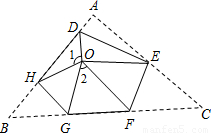
如图，将△ABC三个角分别沿DE、HG、EF翻折，三个顶点均落在点O处，则∠1+∠2的度数为
- A.120°
- B.135°
- C.150°
- D.180°
D
分析：根据翻折变换前后对应角不变，故∠B=∠HOG，∠A=∠DOE，∠C=∠EOF，∠1+∠2+∠HOG+∠EOF+∠DOE=360°，进而求出∠1+∠2的度数．
解答：∵将△ABC三个角分别沿DE、HG、EF翻折，三个顶点均落在点O处，
∴∠B=∠HOG，∠A=∠DOE，∠C=∠EOF，∠1+∠2+∠HOG+∠EOF+∠DOE=360°，
∵∠HOG+∠EOF+∠DOE=∠A+∠B+∠C=180°，
∴∠1+∠2=360°-180°=180°，
故选：D．
点评：此题主要考查了翻折变换的性质和三角形的内角和定理，根据已知得出∠HOG+∠EOF+∠DOE=∠A+∠B+∠C=180°是解题关键．
分析：根据翻折变换前后对应角不变，故∠B=∠HOG，∠A=∠DOE，∠C=∠EOF，∠1+∠2+∠HOG+∠EOF+∠DOE=360°，进而求出∠1+∠2的度数．
解答：∵将△ABC三个角分别沿DE、HG、EF翻折，三个顶点均落在点O处，
∴∠B=∠HOG，∠A=∠DOE，∠C=∠EOF，∠1+∠2+∠HOG+∠EOF+∠DOE=360°，
∵∠HOG+∠EOF+∠DOE=∠A+∠B+∠C=180°，
∴∠1+∠2=360°-180°=180°，
故选：D．
点评：此题主要考查了翻折变换的性质和三角形的内角和定理，根据已知得出∠HOG+∠EOF+∠DOE=∠A+∠B+∠C=180°是解题关键．
练习册系列答案
相关题目
（2012•石家庄二模）如图，将△ABC三个角分别沿DE、HG、EF翻折，三个顶点均落在点O处，则∠1+∠2的度数为（ ）
如图，三角形ABC三个项点坐标分别为A（3，-2），B（0，2），C（0，-5），将三角形ABC沿y轴正方向平移2个单位，再沿x轴负方向平移l个单位，得到三角形A1B1C1．
