题目内容
 (2009•南安市质检)如图,在直角坐标系中,已知点A(0,6),B(8,0).
(2009•南安市质检)如图,在直角坐标系中,已知点A(0,6),B(8,0).(1)直接写出AB的长;
(2)点P(x,0)为线段OB上一动点(点O、B除外),过点P作PQ∥OA交AB于点Q.
①若以线段PQ为直径的⊙M与y轴相切,求点P的坐标;
②把△BPQ沿直线PQ向左侧翻折叠到△CPQ,若△CPQ与梯形OPQA重叠部分的面积为s,求s关于x的函数关系式,并求当x为何值时,s的值最大,最大值是多少?
分析:(1)根据两点间的距离公式可以求得线段AB的长度;
(2)①由平行线分线段成比例知
=
,即
=
;再由圆的切线的性质可以推知
PQ=OP,即
×(6-
x)=x,则以求x的值;
②分类讨论:如图2,当0<x<4时,△CPQ与梯形OPQA重叠的部分是梯形OPQD,根据梯形的面积公式来计算重叠部分的面积即可;
如图3,当4≤x<8时,△CPQ与梯形OPQA重叠部分是△CPQ,根据三角形的面积公式计算重叠部分的面积即可.
(2)①由平行线分线段成比例知
| PQ |
| OA |
| BP |
| PO |
| PQ |
| 6 |
| 8-x |
| 8 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
②分类讨论:如图2,当0<x<4时,△CPQ与梯形OPQA重叠的部分是梯形OPQD,根据梯形的面积公式来计算重叠部分的面积即可;
如图3,当4≤x<8时,△CPQ与梯形OPQA重叠部分是△CPQ,根据三角形的面积公式计算重叠部分的面积即可.
解答: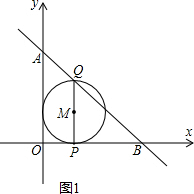 解:(1)∵A(0,6),B(8,0).
解:(1)∵A(0,6),B(8,0).
∴AB=
=10;
(2)①如图1,由题意知,OP=x,则BP=8-x.
∵PQ∥OA,
∴
=
,即
=
,
解得,PQ=6-
x.
当以线段PQ为直径的⊙M与y轴相切时,
PQ=OP,
∴
PQ=OP,即
×(6-
x)=x,
解得,x=
,
则点P的坐标是(
,0);
②如图2,当0<x<4时,∵△CPQ与梯形OPQA重叠的部分是梯形OPQD,则BP=CP=8-x,
∴OC=CP-OP=8-2x.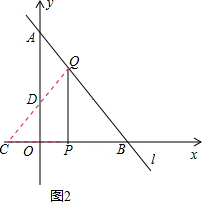
∵OD∥PQ,
∴
=
,即
=
,
解得,OD=6-
x,
∴s=
×(OD+PQ)×OP
=
×(6-
x+6-
x)x
=-
x2+6x
=-
(x-
)2+8.
∵x=
满足题意,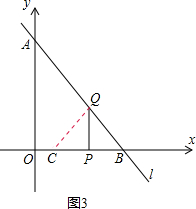
∴当x=
时,s的值最大为8;
如图3,当4≤x<8时,△CPQ与梯形OPQA重叠部分是△CPQ,则
PC=BP=8-x,
∴s=
PC•PQ=
(8-x)×(6-
x)=
(x-8)2.
∵该抛物线的开口方向向上,
∴当4≤x<8时,y随x的增大而减小,
∴当x=4是,s的值最大,最大值为6.
综上所述,s关于x的函数关系式为:s=-
x2+6x(0<x<4);
s=
(x-8)2(4≤x<8);
且当x=
时,s的最大值是8.
 解:(1)∵A(0,6),B(8,0).
解:(1)∵A(0,6),B(8,0).∴AB=
| 62+82 |
(2)①如图1,由题意知,OP=x,则BP=8-x.
∵PQ∥OA,
∴
| PQ |
| OA |
| BP |
| PO |
| PQ |
| 6 |
| 8-x |
| 8 |
解得,PQ=6-
| 3 |
| 4 |
当以线段PQ为直径的⊙M与y轴相切时,
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
解得,x=
| 24 |
| 11 |
则点P的坐标是(
| 24 |
| 11 |
②如图2,当0<x<4时,∵△CPQ与梯形OPQA重叠的部分是梯形OPQD,则BP=CP=8-x,
∴OC=CP-OP=8-2x.

∵OD∥PQ,
∴
| OC |
| PC |
| OD |
| PQ |
| 8-2x |
| 8-x |
| OD | ||
6-
|
解得,OD=6-
| 3 |
| 2 |
∴s=
| 1 |
| 2 |
=
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
=-
| 9 |
| 8 |
=-
| 9 |
| 8 |
| 8 |
| 3 |
∵x=
| 8 |
| 3 |

∴当x=
| 8 |
| 3 |
如图3,当4≤x<8时,△CPQ与梯形OPQA重叠部分是△CPQ,则
PC=BP=8-x,
∴s=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 8 |
∵该抛物线的开口方向向上,
∴当4≤x<8时,y随x的增大而减小,
∴当x=4是,s的值最大,最大值为6.
综上所述,s关于x的函数关系式为:s=-
| 9 |
| 8 |
s=
| 3 |
| 8 |
且当x=
| 8 |
| 3 |
点评:本题综合考查了两点间的距离公式,一次函数图象上点的坐标特征,平行线分线段成比例以及三角形、梯形面积的计算.解答(2)题时,一定要分类讨论,以防漏解.另外,注意数形结合数学思想在解题过程中的运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2009•南安市质检)如图是一座人行天桥的示意图,天桥的高BC为10米,坡面AC的坡角为53°.
(2009•南安市质检)如图是一座人行天桥的示意图,天桥的高BC为10米,坡面AC的坡角为53°.