题目内容
 如图,P是等腰△ABC的底边BC上一点,过点P作BC的垂线,交AB于点Q,交CA的延长线于点R.判断△ARQ是不是等腰三角形,并说明理由.
如图,P是等腰△ABC的底边BC上一点,过点P作BC的垂线,交AB于点Q,交CA的延长线于点R.判断△ARQ是不是等腰三角形,并说明理由.
解:△ARQ是等腰三角形.
理由如下:∵RP⊥BC,
∴∠C+∠R=90°,∠B+∠BQP=90°,
∵AB=AC,
∴∠B=∠C,
∴∠R=∠BQP,
∵∠BQP=∠AQR,
∴∠R=∠AQR,
即△ARQ是等腰三角形.
分析:根据垂直求出∠C+∠R=90°,∠B+∠BQP=90°,再根据等边对等角求出∠B=∠C,从而得到∠R=∠BQP,再根据对顶角相等求出∠BQP=∠AQR,然后求出∠R=∠AQR,根据等角对等边可得AQ=AR,从而判断出△ARQ是等腰三角形.
点评:本题考查了等腰三角形的判定与性质,垂直的定义,熟记等边对等角和等角对等边是解题的关键.
理由如下:∵RP⊥BC,
∴∠C+∠R=90°,∠B+∠BQP=90°,
∵AB=AC,
∴∠B=∠C,
∴∠R=∠BQP,
∵∠BQP=∠AQR,
∴∠R=∠AQR,
即△ARQ是等腰三角形.
分析:根据垂直求出∠C+∠R=90°,∠B+∠BQP=90°,再根据等边对等角求出∠B=∠C,从而得到∠R=∠BQP,再根据对顶角相等求出∠BQP=∠AQR,然后求出∠R=∠AQR,根据等角对等边可得AQ=AR,从而判断出△ARQ是等腰三角形.
点评:本题考查了等腰三角形的判定与性质,垂直的定义,熟记等边对等角和等角对等边是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
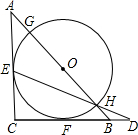 如图,△ABC是等腰直角三角形,AC=BC=a,以斜边AB上的点O为圆心的圆分别与AC、BC相切于点E、F,与AB分别相交于点G、H,且EH的延长线与CB的延长线交于点D,则CD的长为( )
如图,△ABC是等腰直角三角形,AC=BC=a,以斜边AB上的点O为圆心的圆分别与AC、BC相切于点E、F,与AB分别相交于点G、H,且EH的延长线与CB的延长线交于点D,则CD的长为( )A、
| ||||
B、
| ||||
C、
| ||||
D、(
|
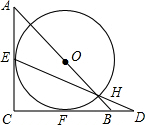 如图,△ABC是等腰直角三角形,AC=BC=2,以斜边AB上的点O为圆心的圆分别与AC、BC相切于点E、F,与AB分别相交于点G、H,且EH的延长线与CB的延长线交于点D,则CD的长为
如图,△ABC是等腰直角三角形,AC=BC=2,以斜边AB上的点O为圆心的圆分别与AC、BC相切于点E、F,与AB分别相交于点G、H,且EH的延长线与CB的延长线交于点D,则CD的长为
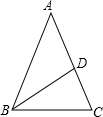
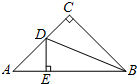 如图,△ABC是等腰直角三角形,∠C=90°,BD平分∠CBA交AC于点D,DE⊥AB于E.若△ADE的周长为8cm,则AB=
如图,△ABC是等腰直角三角形,∠C=90°,BD平分∠CBA交AC于点D,DE⊥AB于E.若△ADE的周长为8cm,则AB=