ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩΡ≥ΙΪΥΨ…ζ≤ζΒΡA÷÷≤ζΤΖΘ§ΟΩΦΰ≥…±Ψ «2‘ΣΘ§ΟΩΦΰ έΦέ «3‘ΣΘ§“ΜΡξΒΡœζ έΝΩ «10ΆρΦΰΘ°ΈΣΝΥΜώΒΟΗϋΕύΒΡάϊ»σΘ§ΙΪΥΨΉΦ±ΗΡΟ≥ω“ΜΕ®Ή Ϋπά¥ΉωΙψΗφΘ°ΗυΨίΨ≠―ιΘ§ΟΩΡξΆΕ»κΒΡΙψΗφΖ―ΈΣxΘ®Άρ‘ΣΘ© ±Θ§≤ζΤΖΒΡΡξœζ έΝΩ «‘≠ά¥ΒΡy±ΕΘ§«“y «xΒΡΕΰ¥ΈΚ· ΐΘ§ΙΪΥΨΉςΝΥ‘Λ≤βΘ§÷Σx”κy÷°ΦδΒΡΕ‘”ΠΙΊœΒ»γ±μΘΚ
![]()
Θ®1Θ©ΗυΨί±μ÷–Θ§«σyΙΊ”ΎxΒΡΚ· ΐΙΊœΒ ΫΘΜ
Θ®2Θ©»γΙϊΑ―άϊ»σΩ¥≥… «œζ έΉήΕνΦθ»Ξ≥…±ΨΚΆΙψΗφΖ―Θ§«κΡψ–¥≥ωΡξάϊ»σSΘ®Άρ‘ΣΘ©”κΙψΗφΖ―xΘ®Άρ‘ΣΘ©ΒΡΚ· ΐΙΊœΒ ΫΘΜ
Θ®3Θ©ΗυΨί…œΟφΒΡΚ· ΐΙΊœΒ ΫΘ§Ρψ»œΈΣΟΩΡξΆΕ»κΕύ…ΌΙψΗφΖ―ΉνΚœ ΘΩΈΣ ≤Ο¥ΘΩ
ΓΨ¥πΑΗΓΩΘ®1Θ©y=©¹![]() x2+
x2+![]() x+1ΘΜΘ®2Θ©S=©¹x2+5x+10Θ®3Θ©ΟΩΡξΆΕ»κΙψΗφΖ―ΈΣ2.5Άρ‘ΣΉνΚœ Θ§“ρΈΣ¥Υ ±Ω…ΜώΉν¥σάϊ»σ
x+1ΘΜΘ®2Θ©S=©¹x2+5x+10Θ®3Θ©ΟΩΡξΆΕ»κΙψΗφΖ―ΈΣ2.5Άρ‘ΣΉνΚœ Θ§“ρΈΣ¥Υ ±Ω…ΜώΉν¥σάϊ»σ
ΓΨΫβΈωΓΩ
‘ΧβΖ÷ΈωΘΚΘ®1Θ©…ηΥυ«σΚ· ΐΙΊœΒ ΫΈΣy=ax2+bx+cΘ§”…±μ÷– ΐΨί”Ο¥ΐΕ®œΒ ΐΖ®Ω…«σΒΟΫβΈω ΫΘΜ
Θ®2Θ©ΗυΨίΘΚΉήάϊ»σ=ΟΩΦΰάϊ»σΓΝœζ έΝΩ©¹ΙψΗφΖ―Ν–Κ· ΐΙΊœΒ ΫΦ¥Ω…ΘΜ
Θ®3Θ©ΫΪΘ®2Θ©÷–Κ· ΐΙΊœΒ Ϋ≈δΖΫ≥…ΕΞΒψ ΫΘ§Ω…÷ΣΜώΒΟΉν¥σάϊ»σ ±ΆΕ»κΒΡΙψΗφΖ―xΘ°
ΫβΘΚΘ®1Θ©…ηΥυ«σΚ· ΐΙΊœΒ ΫΈΣy=ax2+bx+cΘ§
Α―Θ®0Θ§1Θ©Θ§Θ®1Θ§1.5Θ©Θ§Θ®2Θ§1.8Θ©Ζ÷±π¥ζ»κ…œ ΫΘ§
ΒΟΘΚ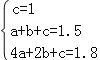 Θ§
Θ§
ΫβΒΟΘΚ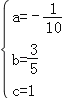 Θ§
Θ§
Γύy=©¹![]() x2+
x2+![]() x+1ΘΜ
x+1ΘΜ
Θ®2Θ©ΗυΨίΧβ“βΘ§”–ΘΚS=Θ®3©¹2Θ©ΓΝ10y©¹x
=Θ®©¹![]() x2+
x2+![]() x+1Θ©ΓΝ10©¹x
x+1Θ©ΓΝ10©¹x
=©¹x2+5x+10ΘΜ
Θ®3Θ©ΓΏS=©¹x2+5x+10=©¹Θ®x©¹![]() Θ©2+
Θ©2+![]() Θ§
Θ§
ΓύΟΩΡξΆΕ»κΙψΗφΖ―ΈΣ2.5Άρ‘ΣΉνΚœ Θ§“ρΈΣ¥Υ ±Ω…ΜώΉν¥σάϊ»σΘ°


