题目内容
 (2012•浙江二模)如图,矩形OABC在平面直角坐标系中,A(0,3),C(4,0),点P为直线AB上一动点,将直线OP绕点P逆时针方向旋转90°交直线BC于点Q,当△POQ为等腰三角形时,点P坐标为
(2012•浙江二模)如图,矩形OABC在平面直角坐标系中,A(0,3),C(4,0),点P为直线AB上一动点,将直线OP绕点P逆时针方向旋转90°交直线BC于点Q,当△POQ为等腰三角形时,点P坐标为P1(1,3),P2(7,3)
P1(1,3),P2(7,3)
.分析:设点P的横坐标为m,因为△POQ是等腰三角形所以PO=PQ,根据等式PA2+AO2=PB2+BQ2可求得m的值,从而就可确定点P的坐标.
解答:解:∵△POQ是等腰三角形,
①若P在线段AB上,∠OPQ=90°
∴PO=PQ,
又∵△OAP∽△PBQ,
∴△OAP≌△PBQ
∴PB=AO,即3=4-m,
∴m=1,即P点坐标(1,3);(8分)
②若P在线段AB的延长线上,PQ交CB的延长线于Q,PO=PQ,
又∵△AOP∽△BPQ,
∴△AOP≌△BPQ,
∴AO=PB,即3=m-4,即P点的坐标(7,3);
③当P在线段BA的延长线上时,显然不成立;
故点P坐标为P1(1,3),P2(7,3).
故答案为:P1(1,3),P2(7,3).
①若P在线段AB上,∠OPQ=90°
∴PO=PQ,
又∵△OAP∽△PBQ,
∴△OAP≌△PBQ
∴PB=AO,即3=4-m,
∴m=1,即P点坐标(1,3);(8分)
②若P在线段AB的延长线上,PQ交CB的延长线于Q,PO=PQ,
又∵△AOP∽△BPQ,
∴△AOP≌△BPQ,
∴AO=PB,即3=m-4,即P点的坐标(7,3);
③当P在线段BA的延长线上时,显然不成立;
故点P坐标为P1(1,3),P2(7,3).
故答案为:P1(1,3),P2(7,3).
点评:此题考查学生对等腰三角形的性质,相似三角形的判定,勾股定理及一次函数等知识点的综合运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
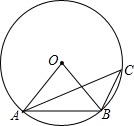 (2012•浙江二模)如图所示,⊙O是△ABC的外接圆.若∠ACB=35°,则∠OBA的度数等于( )
(2012•浙江二模)如图所示,⊙O是△ABC的外接圆.若∠ACB=35°,则∠OBA的度数等于( )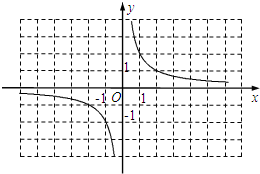 同样可以找到平移规律.
同样可以找到平移规律.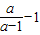 )÷
)÷ .
. )÷
)÷ .
.