题目内容
(2012•浙江二模)我们知道,二次函数y=ax2的图象进行向右或向左平移一次,再向上或向下平移一次可以得到y=a(x+m)2+k的图象.实际上,我们学过的反比例函数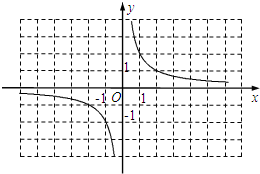 同样可以找到平移规律.
同样可以找到平移规律.
(1)请直接写出函数y=2x2向右平移3个单位,再向上平移1个单位的函数解析式
(2)现在探究反比例函数的平移.探究一:把反比例函数y=
的图象向右平移3个单位,请你至少在图象上取4个不同的点,分别找出平移后的点,通过对这些点的观察、探究、猜想,写出平移后的函数解析式.(写出求解过程)
(3)探究二:一般地,函数y=
(mk≠0)的图象可由哪个反比例函数的图象经过怎样的平移变换得到?
 同样可以找到平移规律.
同样可以找到平移规律.(1)请直接写出函数y=2x2向右平移3个单位,再向上平移1个单位的函数解析式
y=2(x-3)2+1
y=2(x-3)2+1
.(2)现在探究反比例函数的平移.探究一:把反比例函数y=
| 2 |
| x |
(3)探究二:一般地,函数y=
| k |
| x+m |
分析:(1)根据二次函数平移的规律:左加右减,上加下减即可得到函数y=2x2向右平移3个单位,再向上平移1个单位的函数解析式;
(2)先在反比例函数y=
的图象上取四个点(0.5,4),(1,2),(1.5,
),(2,1),再根据坐标系中点的平移规律,得到向右平移3个单位以后的对应点的坐标,然后对这些点的坐标进行观察,得到平移后的函数解析式;
(3)由(2)即可得到函数y=
(mk≠0)的图象可由反比例函数y=
的图象向左平移m个单位得到.
(2)先在反比例函数y=
| 2 |
| x |
| 4 |
| 3 |
(3)由(2)即可得到函数y=
| k |
| x+m |
| k |
| x |
解答:解:(1)将二次函数y=2x2的图象向右平移3个单位,再向上平移1个单位后,
所得图象的函数解析式是:y=2(x-3)2+1.
故答案为:y=2(x-3)2+1;
(2)在反比例函数y=
的图象上取四个点(0.5,4),(1,2),(1.5,
),(2,1),
则向右平移3个单位以后的对应点的坐标为(3.5,4),(4,2),(4.5,
),(5,1),
∵(3.5-3)×4=(4-3)×2=(4.5-3)×
=(5-3)×1=2,
∴平移后的函数解析式为y=
;
(3)函数y=
(mk≠0)的图象可由反比例函数y=
的图象向左平移m个单位得到.
所得图象的函数解析式是:y=2(x-3)2+1.
故答案为:y=2(x-3)2+1;
(2)在反比例函数y=
| 2 |
| x |
| 4 |
| 3 |
则向右平移3个单位以后的对应点的坐标为(3.5,4),(4,2),(4.5,
| 4 |
| 3 |
∵(3.5-3)×4=(4-3)×2=(4.5-3)×
| 4 |
| 3 |
∴平移后的函数解析式为y=
| 2 |
| x-3 |
(3)函数y=
| k |
| x+m |
| k |
| x |
点评:本题考查了学生读题做题的能力及知识的迁移能力,二次函数解析式平移的规律:“上加下减,左加右减”也适用于反比例函数的解析式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
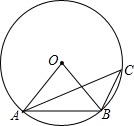 (2012•浙江二模)如图所示,⊙O是△ABC的外接圆.若∠ACB=35°,则∠OBA的度数等于( )
(2012•浙江二模)如图所示,⊙O是△ABC的外接圆.若∠ACB=35°,则∠OBA的度数等于( ) (2012•浙江二模)如图,矩形OABC在平面直角坐标系中,A(0,3),C(4,0),点P为直线AB上一动点,将直线OP绕点P逆时针方向旋转90°交直线BC于点Q,当△POQ为等腰三角形时,点P坐标为
(2012•浙江二模)如图,矩形OABC在平面直角坐标系中,A(0,3),C(4,0),点P为直线AB上一动点,将直线OP绕点P逆时针方向旋转90°交直线BC于点Q,当△POQ为等腰三角形时,点P坐标为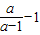 )÷
)÷ .
. )÷
)÷ .
.