题目内容
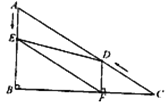
【题目】如图,在四边形ABCD中,AB=DC,E,F,G,H分别是AD,BC,BD,AC的中点.
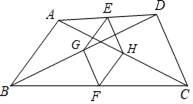
(1)证明:EG=EH;(2)证明:四边形EHFG是菱形.
【答案】(1)见解析;(2)见解析.
【解析】
(1)利用EG是△ABD的中位线,EH是△ADC的中位线,则有EG=![]() AB,EH=
AB,EH=![]() CD,又AB=CD,可证EG=EH,即可解题.
CD,又AB=CD,可证EG=EH,即可解题.
(2)首先运用三角形中位线定理可得到EG∥AB,HF∥AB,EH∥CD,FE∥DC,从而再根据平行于同一条直线的两直线平行得到GF∥EH,GE∥FH,可得到GFHE是平行四边形,再运用三角形中位线定理证明邻边相等,从而证明它是菱形.
解:证明:(1)∵四边形ABCD中,点F、E、G、H分别是BC、AD、BD、AC的中点,
∴EG是△ABD的中位线,EH是△ADC的中位线,
∴EG=![]() AB,EH=
AB,EH=![]() CD,
CD,
∵AB=CD,
∴EG=EH;
(2)∵四边形ABCD中,点F、E、G、H分别是BC、AD、BD、AC的中点,
∴EG∥AB,HF∥AB,EH∥CD,FE∥DC,
∴GF∥EH,GE∥FH(平行于同一条直线的两直线平行);
∴四边形GFHE是平行四边形,
∵四边形ABCD中,点E、F、G、H分别是BC、AD、BD、AC的中点,
∴EG是△ABD的中位线,GF是△BCD的中位线,
∴GE=![]() AB,GF=
AB,GF=![]() CD,
CD,
∵AB=CD,
∴GE=GF,
∴四边形EHFG是菱形.

练习册系列答案
相关题目