题目内容
【题目】如图所示,A,B两地相距50千米,甲于某日下午1时骑自行车从A地出发驶往B地,乙也于同日下午2时骑摩托车按同路从A地出发驶往B地,图中的折线PQR和线段MN分别表示甲、乙所行驶的路程S与该日下午行驶的时间t之间的关系.根据图象回答下列问题: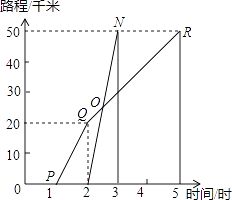
(1)甲在该日下午2﹣5时骑自行车的速度是多少?
(2)乙从出发大约用多长时间就能追上甲?
(3)甲骑自行车和乙骑摩托车在全程的平均速度分别是多少?
【答案】
(1)解:甲在该日下午2﹣5时骑自行车的速度是 ![]() =10千米/小时
=10千米/小时
(2)解:由图可知:M(2,0),N(3,50),Q(2,20),R(5,50)
设直线QR的函数表达式为y1=k1x+b1,
将Q(2,20),R(5,50)代入得:
![]() ,
,
解得 ![]() ,
,
设直线MN的函数表达式为y2=k2x+b2,
将M(2,0),N(3,50)代入得:
![]() ,
,
解得 ![]() ,
,
则y1=10x,y2=50x﹣100,
联立两式可得直线QR、MN的交点的坐标为(2.5,25).
所以乙出发半小时后追上甲
(3)解:乙的平均速度为 ![]() =50千米/时,甲的平均速度为
=50千米/时,甲的平均速度为 ![]() =12.5千米/时
=12.5千米/时
【解析】(1)根据速度=路程÷时间即可解决问题;
(2)先求得两函数的解析式,然后再组成方程组,求得两个函数交点的坐标即可;
(3)用各自的总路程÷各自的总时间,列式计算即可求解.

练习册系列答案
相关题目