题目内容
 (1)比较大小:
(1)比较大小:
①3+5______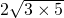 ;
;
②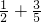 ______
______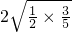 ;
;
③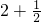 ______
______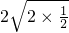 ;④6+6______
;④6+6______ .
.
(2)通过(1)的判断,你可猜想:当a、b为正实数时,a+b与 的大小关系为a+b______
的大小关系为a+b______ .
.
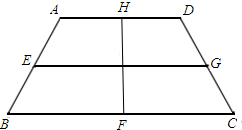
(3)利用上述猜想解决下列问题:如图,有一等腰梯形的工件(厚度不计),其面积为1800cm2,现要用包装带如图包扎(四点为四边中点),求最少需要包装带的长为多少cm?
解:(1)①∵3+5=8=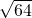 ,
,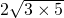 =
=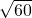 ,
,
∴3+5>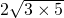 ;
;
②∵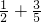 =
=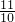 =
= ,2
,2 =
= ,
,
∴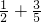 >
>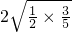 ;
;
③∵2+ =
= =
=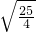 ,
,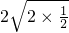 =
= ,
,
∴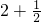 >
>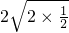 ;
;
④∵6+6=12=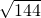 ,2
,2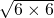 =
=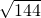 ,
,
∴6+6=2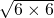 ;
;
(2)由上面的例子得a+b≥2 ,理由如下:
,理由如下:
∵(a-b)2≥0,∴a2+b2-2ab≥0,a2+b2-2ab+4ab≥0+4ab,
∴(a+b)2≥4ab,即a+b≥2 ;
;
(3)∵S梯形ACBD= =1800,梯形的中位线=
=1800,梯形的中位线= ,
,
∴梯形的面积=梯形的中位线×高,即中位线×高=1800,
∴EG•HF=1800,
EG+HF≥2 =2
=2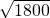 =60
=60 cm,
cm,
答:最少需要包装带的长为60 cm.
cm.
分析:(1)计算出结果,直接比较大小;
(2)由完全平方公式(a-b)2≥0,推得结论;
(3)S梯形ACBD= ,梯形的中位线=
,梯形的中位线= ,则梯形的面积=梯形的中位线×高,即中位线×高=1800,
,则梯形的面积=梯形的中位线×高,即中位线×高=1800,
由(2)得EG+HF≥2 ,即得答案.
,即得答案.
点评:本题考查有理数的大小比较及其实际应用,及利用梯形的第二个面积公式求解问题:梯形的面积=梯形的中位线×高.
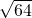 ,
,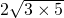 =
=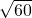 ,
,∴3+5>
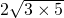 ;
;②∵
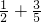 =
=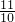 =
= ,2
,2 =
= ,
,∴
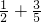 >
>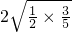 ;
;③∵2+
 =
= =
=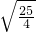 ,
,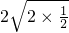 =
= ,
,∴
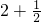 >
>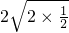 ;
;④∵6+6=12=
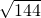 ,2
,2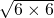 =
=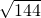 ,
,∴6+6=2
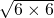 ;
;(2)由上面的例子得a+b≥2
 ,理由如下:
,理由如下:∵(a-b)2≥0,∴a2+b2-2ab≥0,a2+b2-2ab+4ab≥0+4ab,
∴(a+b)2≥4ab,即a+b≥2
 ;
;(3)∵S梯形ACBD=
 =1800,梯形的中位线=
=1800,梯形的中位线= ,
,∴梯形的面积=梯形的中位线×高,即中位线×高=1800,
∴EG•HF=1800,
EG+HF≥2
 =2
=2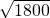 =60
=60 cm,
cm,答:最少需要包装带的长为60
 cm.
cm.分析:(1)计算出结果,直接比较大小;
(2)由完全平方公式(a-b)2≥0,推得结论;
(3)S梯形ACBD=
 ,梯形的中位线=
,梯形的中位线= ,则梯形的面积=梯形的中位线×高,即中位线×高=1800,
,则梯形的面积=梯形的中位线×高,即中位线×高=1800,由(2)得EG+HF≥2
 ,即得答案.
,即得答案.点评:本题考查有理数的大小比较及其实际应用,及利用梯形的第二个面积公式求解问题:梯形的面积=梯形的中位线×高.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目