题目内容
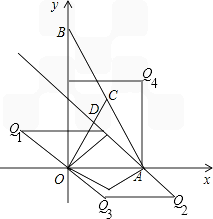
如下图,在平面直角坐标系中,点A、B分别在x轴、y轴上,线段OA、OB的长(0A<OB)是方程组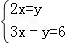 的解,点C是直线y=2x与直线AB的交点,点D在线段OC上,OD=
的解,点C是直线y=2x与直线AB的交点,点D在线段OC上,OD=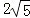 。
。
(1)求直线AB的解析式及点C的坐标;
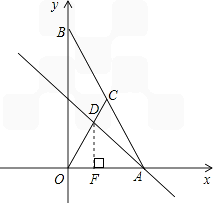
(2)求直线AD的解析式;
(3)P是直线AD上的点,在平面内是否存在点Q,使以0、A、P、Q为顶点的四边形是菱形?若存在,请直接写出点Q的坐标;若不存在,请说明理由。
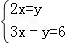 的解,点C是直线y=2x与直线AB的交点,点D在线段OC上,OD=
的解,点C是直线y=2x与直线AB的交点,点D在线段OC上,OD=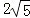 。
。(1)求直线AB的解析式及点C的坐标;
(2)求直线AD的解析式;
(3)P是直线AD上的点,在平面内是否存在点Q,使以0、A、P、Q为顶点的四边形是菱形?若存在,请直接写出点Q的坐标;若不存在,请说明理由。

解:(1)解方程组方程组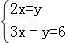 ,
,
解得: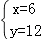
∵线段OA、OB的长(0A<OB)是方程组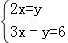 的解,
的解,
∴OA=6,OB=12,
∴A(6,O),B(0,12),
设直线AB的解析为y=kx+b,
∴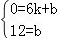
∴直线AB:y=﹣2x+12,
联立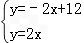 ,
,
解得: ,
,
点C的坐标为(3,6);
(2)设点D:(a,2a),
由OD=2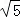 :a2+(2a)2=(2
:a2+(2a)2=(2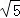 )2,得:a=2,
)2,得:a=2,
∴D:(2,4),
设直线AD的解析式为y=kx+b
把A(6,0),D(2,4)代入得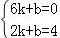 ,
,
解得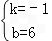 ,
,
∴直线AD的解析式为y=﹣x+6;
(3)存在。
Q1(﹣3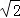 ,3
,3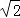 )
)
Q2(3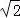 ,﹣3
,﹣3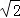 )
)
Q3(3,﹣3)
Q4(6,6)
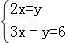 ,
,解得:
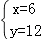
∵线段OA、OB的长(0A<OB)是方程组
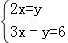 的解,
的解,∴OA=6,OB=12,
∴A(6,O),B(0,12),
设直线AB的解析为y=kx+b,
∴
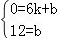
∴直线AB:y=﹣2x+12,
联立
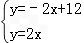 ,
,解得:
 ,
,点C的坐标为(3,6);
(2)设点D:(a,2a),
由OD=2
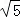 :a2+(2a)2=(2
:a2+(2a)2=(2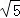 )2,得:a=2,
)2,得:a=2,∴D:(2,4),
设直线AD的解析式为y=kx+b
把A(6,0),D(2,4)代入得
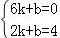 ,
,解得
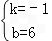 ,
,∴直线AD的解析式为y=﹣x+6;
(3)存在。
Q1(﹣3
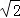 ,3
,3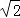 )
)Q2(3
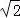 ,﹣3
,﹣3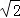 )
)Q3(3,﹣3)
Q4(6,6)



练习册系列答案
相关题目
 7、如下图,在平面直角坐标系中,A点坐标为(-4,3),将线段OA绕原点O顺时针旋转90°得到OA′,则点A′的坐标是( )
7、如下图,在平面直角坐标系中,A点坐标为(-4,3),将线段OA绕原点O顺时针旋转90°得到OA′,则点A′的坐标是( )

 的图像与反比例函数
的图像与反比例函数 的图像交于二、四象限的A、B两点,与x轴交于C点。已知A(-2,m),B(n,-2),
的图像交于二、四象限的A、B两点,与x轴交于C点。已知A(-2,m),B(n,-2), ,则此一次函数的解析式为 .
,则此一次函数的解析式为 .
