题目内容
【题目】如图1,已知□ABCD,AB//x轴,AB=6,点A的坐标为(1,-4),点D的坐标为(-3,4),点B在第四象限,点P是□ABCD边上的一个动点.

(1)若点P在边BC上,PD=CD,求点P的坐标.
(2)若点P在边AB,AD上,点P关于坐标轴对称的点Q落在直线y=x-1上,求点P的坐标.
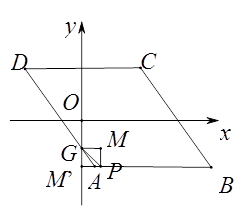
(3)若点P在边AB,AD,CD上,点G是AD与y轴的交点,如图2,过点P作y轴的平行线PM,过点G作x轴的平行线GM,它们相交于点M,将△PGM沿直线PG翻折,当点M的对应点落在坐标轴上时,求点P的坐标(直接写出答案).
【答案】
(1)
解:在□ABCD中, CD=AB=6,
所以点P与点C重合,
所以点P的坐标为(3,4).
(2)
解:①当点P在边AD上时,
由已知得,直线AD的函数表达式为y=-2x-2,
设P(a,-2a-2),且-3≤a≤1,
若点P关于x轴对称点Q1(a,2a+2)在直线y=x-1上,
所以2a+2=a-1,解得a=-3,此时P(-3,4)。
若点P关于y轴对称点Q2(-a,-2a-2)在直线y=x-1上,
所以-2a-2=-a-1,解得a=-1,此时P(-1,0).
②当点P在边AB上时,设P(a,-4),且1≤a≤7,
若点P关于x轴对称点Q3(a,4)在直线y=x-1上,
所以4=a-1,解得a=5,此时P(5,-4).
若点P关于y轴对称点Q4(-a,-4)在直线y=x-1上,
所以-4=-a-1,解得a=3,此时P(3,-4).
综上所述,点P的坐标为(-3,4)或(-1,0)或(5,-4)或(3,-4).
(3)
解:因为直线AD为y=-2x-2,所以G(0,-2).
①如图,当点P在CD边上时,可设P(m,4),且-3≤m≤3,
则可得M′P=PM=4+2=6,M′G=GM=|m|,
易证得△OGM′~△HM′P,
则 ![]() ,
,
即 ![]() ,
,
则OM′= ![]() ,
,
在Rt△OGM′中,
由勾股定理得, ![]() ,
,
解得m= ![]() 或
或 ![]() ,
,
则P( ![]() ,4)或(
,4)或( ![]() ,4);
,4);
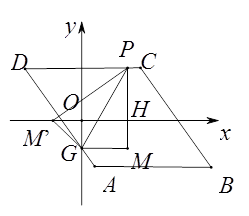
②如下图,当点P在AD边上时,设P(m,-2m-2),
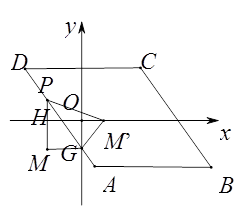
则PM′=PM=|-2m|,GM′=MG=|m|,
易证得△OGM′~△HM′P,
则 ![]() ,
,
即 ![]() ,
,
则OM′= ![]() ,
,
在Rt△OGM′中,
由勾股定理得, ![]() ,
,
整理得m= ![]() ,
,
则P( ![]() ,3);
,3);
如下图,当点P在AB边上时,设P(m,-4),
此时M′在y轴上,则四边形PM′GM是正方形,
所以GM=PM=4-2=2,
则P(2,-4).
综上所述,点P的坐标为(2,-4)或( ![]() ,3)或(
,3)或( ![]() ,4)或(
,4)或( ![]() ,4).
,4).
【解析】(1)点P在BC上,要使PD=CD,只有P与C重合;(2)首先要分点P在边AB,AD上时讨论,根据“点P关于坐标轴对称的点Q”,即还要细分“点P关于x轴的对称点Q和点P关于y轴的对称点Q”讨论,根据关于x轴、y轴对称点的特征(关于x轴对称时,点的横坐标不变,纵坐标变成相反数;关于y轴对称时,相反;)将得到的点Q的坐标代入直线y=x-1,即可解答;(3)在不同边上,根据图象,点M翻折后,点M’落在x轴还是y轴,可运用相似求解.
【考点精析】解答此题的关键在于理解平行四边形的性质的相关知识,掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分,以及对翻折变换(折叠问题)的理解,了解折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.

 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案