题目内容
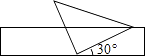
【题目】现有一个“Z”型的工件(工件厚度忽略不计),如图示,其中AB为20cm,BC为60cm,∠ABC=90°,∠BCD=50°,求该工件如图摆放时的高度(即A到CD的距离).(结果精确到0.1m,参考数据:sin50°≈0.766,cos50°≈0.643,tan50°≈1.192) 
【答案】解:如图,过点A作AP⊥CD于点P,交BC于点Q, 
∵∠CQP=∠AQB,∠CPQ=∠B=90°,
∴∠A=∠C=50°,
在△ABQ中,∵AQ= ![]() =
= ![]() ≈31.10,BQ=ABtanA=20tan50°≈23.84,
≈31.10,BQ=ABtanA=20tan50°≈23.84,
∴CQ=BC﹣BQ=60﹣23.84=36.16,
在△CPQ中,∵PQ=CQsinC=36.16sin50°≈27.70,
∴AP=AQ+PQ=27.70+31.10≈58.8,
答:工件如图摆放时的高度约为58.8cm
【解析】.过点A作AP⊥CD于点P,交BC于点Q,由∠CQP=∠AQB、∠CPQ=∠B=90°知∠A=∠C=50°,在△ABQ中求得分别求得AQ、BQ的长,结合BC知CQ的长,在△CPQ中可得PQ,根据AP=AQ+PQ得出答案.

练习册系列答案
相关题目