Question

边长为4的正△AOB的OA边在x轴的正半轴上，点B在第一象限，如图所示，一双曲线分别交AB、OB于D、C两点，其中D为AB中点
（1）求双曲线的解析式；
（2）将△AOB向右平移，当C为OB中点时，求平移的距离．

Answer 1

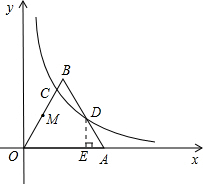解：（1）作DE⊥x轴于E．
根据题意，得AD=2，∠OAD=60°，
∴AE=1，DE=，
∴OE=3，
即D（3，），
设双曲线的解析式是y=（k≠0），
把D（3，）代入，得k=3，
∴y=；

（2）设OB的中点是M，
根据等边三角形的性质和直角三角形的性质得M（1，），
设点M向右平移了a个单位长度，
则有M′（1+a，），
代入（1）中的解析式，
∴=，
∴a=2．
∴平移距离为2．
分析：（1）要求双曲线的解析式，关键是求得点D的坐标，作DE⊥x轴于E，根据等边三角形的性质和30度的直角三角形的性质即可求得DE，AE的长，进一步求得点D的坐标，运用待定系数法即可求解；
（2）首先求得OB的中点坐标，设向右平移了a个单位长度，进一步表示出其对应点的坐标，根据（1）的解析式即可求解．
点评：此题能够熟练运用等边三角形的性质和30度的直角三角形的性质进行计算．注意平移和坐标之间的变化关系：左减右加．