题目内容
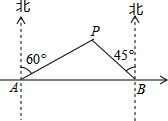 如图,在东西方向的海岸线上有A、B两个港口,甲货船从A港沿北偏东60°的方向以4海里/小时的速度出发,同时乙货船从B港沿西北方向出发,2小时后相遇在点P处,问乙货船每小时航行多少海里?
如图,在东西方向的海岸线上有A、B两个港口,甲货船从A港沿北偏东60°的方向以4海里/小时的速度出发,同时乙货船从B港沿西北方向出发,2小时后相遇在点P处,问乙货船每小时航行多少海里?分析:先作PC⊥AB于点C,根据甲货船从A港沿北偏东60°的方向以4海里/小时的速度出发,求出∠PAC和AP,从而得出PC的值,根据乙货船从B港沿西北方向出发,求出∠PBC=45°,得出PB的值,即可求出答案.
解答: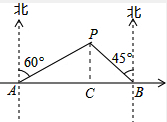 解:作PC⊥AB于点C,
解:作PC⊥AB于点C,
∵甲货船从A港沿北偏东60°的方向以4海里/小时的速度出发,
∴∠PAC=30°,AP=4×2=8,
∴PC=AP×sin30°=8×
=4.
∵乙货船从B港沿西北方向出发,
∴∠PBC=45°,
∴PB=PC÷
=4
,
∴乙货船每小时航行4
÷2=2
海里/小时,
答:乙货船每小时航行2
海里.
 解:作PC⊥AB于点C,
解:作PC⊥AB于点C,∵甲货船从A港沿北偏东60°的方向以4海里/小时的速度出发,
∴∠PAC=30°,AP=4×2=8,
∴PC=AP×sin30°=8×
| 1 |
| 2 |
∵乙货船从B港沿西北方向出发,
∴∠PBC=45°,
∴PB=PC÷
| ||
| 2 |
| 2 |
∴乙货船每小时航行4
| 2 |
| 2 |
答:乙货船每小时航行2
| 2 |
点评:本题考查了解直角三角形的应用,解题的关键是从实际问题中整理出直角三角形并利用解直角三角形的知识求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
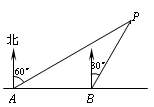
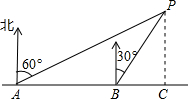 如图,小明同学在东西方向的环海路A处,测得海中灯塔P在北偏东60°方向上,在A处东500米的B处,测得海中灯塔P在北偏东30°方向上,则灯塔P到环海路的距离PC=( )米.
如图,小明同学在东西方向的环海路A处,测得海中灯塔P在北偏东60°方向上,在A处东500米的B处,测得海中灯塔P在北偏东30°方向上,则灯塔P到环海路的距离PC=( )米.| A、250 | ||
| B、500 | ||
C、250
| ||
D、500
|
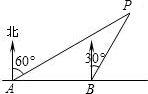 如图,李明同学在东西方向的滨海路A处,测得海中灯塔P在北偏东60°方向上,他向东走400米至B处,测得灯塔P在北偏东30°方向上,求灯塔P到滨海路的距离.(结果保留根号)
如图,李明同学在东西方向的滨海路A处,测得海中灯塔P在北偏东60°方向上,他向东走400米至B处,测得灯塔P在北偏东30°方向上,求灯塔P到滨海路的距离.(结果保留根号)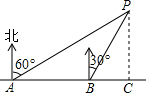 如图,小明同学在东西方向的环海路A处,测得海中灯塔P在北偏东60°方向上,在A处东500米的B处,测得海中灯塔P在北偏东30°方向上,则灯塔P到环海路的距离PC=
如图,小明同学在东西方向的环海路A处,测得海中灯塔P在北偏东60°方向上,在A处东500米的B处,测得海中灯塔P在北偏东30°方向上,则灯塔P到环海路的距离PC=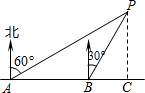 如图,小明同学在东西方向的环海路A处,测得海中灯塔P在北偏东60°方向上,在A处正东500米的B处,测得海中灯塔P在北偏东30°方向上,则灯塔P到环海路的距离PC等于多少米?
如图,小明同学在东西方向的环海路A处,测得海中灯塔P在北偏东60°方向上,在A处正东500米的B处,测得海中灯塔P在北偏东30°方向上,则灯塔P到环海路的距离PC等于多少米?