题目内容
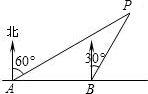 如图,李明同学在东西方向的滨海路A处,测得海中灯塔P在北偏东60°方向上,他向东走400米至B处,测得灯塔P在北偏东30°方向上,求灯塔P到滨海路的距离.(结果保留根号)
如图,李明同学在东西方向的滨海路A处,测得海中灯塔P在北偏东60°方向上,他向东走400米至B处,测得灯塔P在北偏东30°方向上,求灯塔P到滨海路的距离.(结果保留根号)
分析:过P作AB的垂线,设垂足为C.易知∠BAP=30°,∠PBC=60°.∠BPA=∠BAP=30°,得PB=AB=400;
在Rt△PBC中,可用正弦函数求出PC的长.
在Rt△PBC中,可用正弦函数求出PC的长.
解答: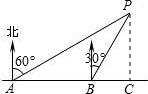 解:过点P作PC⊥AB,垂足为C. (1分)
解:过点P作PC⊥AB,垂足为C. (1分)
由题意,得∠PAB=30°,∠PBC=60°.
∵∠PBC是△APB的一个外角,
∴∠APB=∠PBC-∠PAB=30°. (3分)
∴∠PAB=∠APB,(4分)
故AB=PB=400. (6分)
在Rt△PBC中,∠PCB=90°,∠PBC=60°,PB=400,
∴PC=PB•sin60°=400×
=200
米. (10分)
 解:过点P作PC⊥AB,垂足为C. (1分)
解:过点P作PC⊥AB,垂足为C. (1分)由题意,得∠PAB=30°,∠PBC=60°.
∵∠PBC是△APB的一个外角,
∴∠APB=∠PBC-∠PAB=30°. (3分)
∴∠PAB=∠APB,(4分)
故AB=PB=400. (6分)
在Rt△PBC中,∠PCB=90°,∠PBC=60°,PB=400,
∴PC=PB•sin60°=400×
| ||
| 2 |
| 3 |
点评:本题主要考查了方向角含义,能够发现△PBA是等腰三角形,并正确的构建出直角三角形是解答此题的关键.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目



