题目内容
【题目】在![]() 和
和![]() 中,
中,![]() .点
.点![]() 在
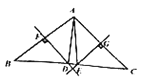
在![]() 上,BC、ED相交于点F,FE=FC,AB=DC,CF平分∠ACE.
上,BC、ED相交于点F,FE=FC,AB=DC,CF平分∠ACE.

(1)![]() 与
与![]() 相等吗?请说明理由;
相等吗?请说明理由;
(2)请说明![]() 是
是![]() 中点的理由.
中点的理由.
【答案】(1)相等,理由见解析;(2)见解析。
【解析】
(1)要判断BC和DE是否相等,可以证明△ABC≌△CDE即可。(2)要说明D为AC中点,因为第一问的全等可知AB为AC的一半,所以可以证明30°来求解。
∵CF平分∠ACE;
∴∠ACB=∠ ECB
∵FE=FC
∴∠E=∠ECB
∴∠ACB=∠E。
在△△ABC和△CDE中
∠ACB=∠E
∠B=∠EDC
AB=CD
∴△ABC≌△CDE(AAS)
∴BC=DE
(2)∵∠ B=90°,∠ACB=∠E=∠ECB
∴∠ACB=∠E=∠ECB=30°
∴AC=2AB(直角三角形中30°所对的直角边是斜边的一半)
又AB=CD,
∴D是AC的中点。

练习册系列答案
相关题目