题目内容
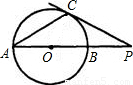
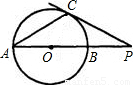
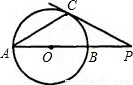
（2006•绍兴）已知⊙O的直径AB与弦AC的夹角为35°，过C点的切线PC与AB的延长线交于点P，则∠P等于（ ）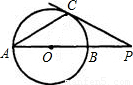
A．15°
B．20°
C．25°
D．30°
【答案】分析：先由PC为⊙O的切线得出∠PCO=90°，再用等腰三角形性质求出∠ACO=∠PAC=35°，最后利用三角形内角和即可求解．
解答：
解：连接OC，PC为⊙O的切线，所以∠PCO=90°，
因为OA=OC，则∠ACO=∠PAC=35°，
在△ACP中，∠P=180°-35°-35°-90°=20°．
故选B．
点评：本题是考查圆的切线的性质、等腰三角形性质、三角形内角和的综合运用能力．
解答：
解：连接OC，PC为⊙O的切线，所以∠PCO=90°，因为OA=OC，则∠ACO=∠PAC=35°，
在△ACP中，∠P=180°-35°-35°-90°=20°．
故选B．
点评：本题是考查圆的切线的性质、等腰三角形性质、三角形内角和的综合运用能力．
练习册系列答案
培优三好生系列答案
优化作业上海科技文献出版社系列答案
相关题目
