题目内容
若一个矩形的短边与长边的比值为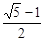 (黄金分割数),我们把这样的矩形叫做黄金矩形.
(黄金分割数),我们把这样的矩形叫做黄金矩形.

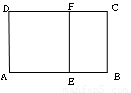
(1)操作:请你在如图所示的黄金矩形ABCD(AB>AD)中,以短边AD为一边作正方形AEFD;
(2)探究:在(1)中的四边形EBCF是不是黄金矩形?若是,请予以证明;若不是,请说明理由.
【答案】
(1) (2)四边形EBCF是是黄金矩形,理由见解析
(2)四边形EBCF是是黄金矩形,理由见解析
【解析】解(1)
(2)答:四边形EBCF是是黄金矩形. …………………4分
证明:∵四边形AEFD是正方形,
∴∠AEF=90° ,∴∠BEF=90°,
∵四边形ABCD是矩形,
∴∠B=∠C=90°
∴∠BEF=∠B=∠C=90°,∴四边形EBCF是矩形. …………………6分
设CD=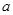 , AD=b,则有
, AD=b,则有
 ∴
∴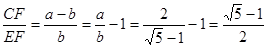 ………8分
………8分
∴矩形EBCF是黄金矩形. …………………9分
(1)只需在矩形的长上截取AE=AD,DF=AD,连接EF即可,
(2)可以结合(1)中正方形的性质求得矩形EBCF的宽与长的比进行分析.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
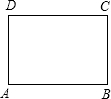 若一个矩形的短边与长边的比值为
若一个矩形的短边与长边的比值为 我们已经知道,如果线段MN被点P分成线段MP和PN,且
我们已经知道,如果线段MN被点P分成线段MP和PN,且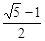 (黄金分割数),我们把这样的矩形叫做黄金矩形.
(黄金分割数),我们把这样的矩形叫做黄金矩形.
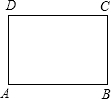 若一个矩形的短边与长边的比值为
若一个矩形的短边与长边的比值为 (黄金分割数),我们把这样的矩形叫做黄金矩形.
(黄金分割数),我们把这样的矩形叫做黄金矩形.