题目内容
 若一个矩形的短边与长边的比值为
若一个矩形的短边与长边的比值为
| ||
| 2 |
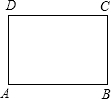
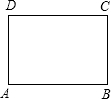
(1)操作:请你在如图所示的黄金矩形ABCD(AB>AD)中,以短边AD为一边作正方形AEFD;
(2)探究:在(1)中的四边形EBCF是不是黄金矩形?若是,请予以证明;若不是,请说明理由.
分析:(1)只需在矩形的长上截取AE=AD,DF=AD,连接EF即可,
(2)可以结合(1)中正方形的性质求得矩形EBCF的宽与长的比进行分析.
(2)可以结合(1)中正方形的性质求得矩形EBCF的宽与长的比进行分析.
解答: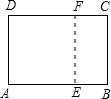 解:(1)如图:以A为圆心,在AB上截取AE=AD,
解:(1)如图:以A为圆心,在AB上截取AE=AD,
以D为圆心,在DC上截取DF=DA,
连接EF,
所以四边形AEFD为所求作的正方形;
(2)答:四边形EBCF是黄金矩形.
证明:∵四边形AEFD是正方形,
∴∠AEF=90°,
∴∠BEF=90°,
∵四边形ABCD是矩形,
∴∠B=∠C=90°
∴∠BEF=∠B=∠C=90°,
∴四边形EBCF是矩形.
设CD=a,AD=b,则有
=
,
∴
=
=
-1=
-1=
,
∴矩形EBCF是黄金矩形.
 解:(1)如图:以A为圆心,在AB上截取AE=AD,
解:(1)如图:以A为圆心,在AB上截取AE=AD,以D为圆心,在DC上截取DF=DA,
连接EF,
所以四边形AEFD为所求作的正方形;
(2)答:四边形EBCF是黄金矩形.
证明:∵四边形AEFD是正方形,
∴∠AEF=90°,
∴∠BEF=90°,
∵四边形ABCD是矩形,
∴∠B=∠C=90°
∴∠BEF=∠B=∠C=90°,
∴四边形EBCF是矩形.
设CD=a,AD=b,则有
| b |
| a |
| ||
| 2 |
∴
| CF |
| EF |
| a-b |
| b |
| a |
| b |
| 2 | ||
|
| ||
| 2 |
∴矩形EBCF是黄金矩形.
点评:本题主要考查了正方形的性质和黄金矩形的概念,综合性较强,难度适中.

练习册系列答案
相关题目
 我们已经知道,如果线段MN被点P分成线段MP和PN,且
我们已经知道,如果线段MN被点P分成线段MP和PN,且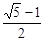 (黄金分割数),我们把这样的矩形叫做黄金矩形.
(黄金分割数),我们把这样的矩形叫做黄金矩形.
 若一个矩形的短边与长边的比值为
若一个矩形的短边与长边的比值为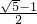 (黄金分割数),我们把这样的矩形叫做黄金矩形.
(黄金分割数),我们把这样的矩形叫做黄金矩形.