题目内容
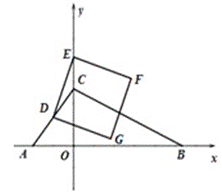
【题目】如图,在平面直角坐标系中,直线![]() 分别交x轴,y轴于点A,C,点D(m,4)在直线AC上,点B在x轴正半轴上,且OB=2OC.点E是y轴上任意一点,连结DE,将线段DE按顺时针旋转90°得线段DG,作正方形DEFG,记点E为(0,n).
分别交x轴,y轴于点A,C,点D(m,4)在直线AC上,点B在x轴正半轴上,且OB=2OC.点E是y轴上任意一点,连结DE,将线段DE按顺时针旋转90°得线段DG,作正方形DEFG,记点E为(0,n).
(1)求点D的坐标;
(2)记正方形DEFG的面积为S,
① 求S关于n的函数关系式;
② 当DF∥x轴时,求S的值;
(3)是否存在n的值,使正方形的顶点F或G落在△ABC的边上?若存在,求出所有满足条件的n的值;若不存在,说明理由.
【答案】(1)点D的坐标为(-3,4);(2)①S=(n-4)2+9;②S=(7-4)2+9=18;当n=![]() 或21或3或
或21或3或![]() 时,正方形的顶点F或G落在△ABC的边上.
时,正方形的顶点F或G落在△ABC的边上.
【解析】试题分析:(1)由于点D(m,4)在直线AC上,代入直线AC的解析式可得关于m的方程,解方程即可得到点D的坐标为(﹣3,4);
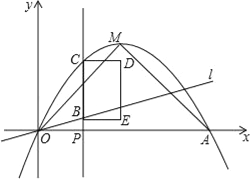
(2)①如图1,过点D作DH⊥y轴于H,则EH=|n﹣4|,根据正方形的面积公式和勾股定理可得S关于n的函数关系式;
②当DF∥x轴时,点H即为正方形DEFG的中心,可得n=7,再代入函数关系式即可得到S的值;
(3)根据待定系数法可得BC为: ![]() ;再分四种情况:①当点F落在BC边上时;②当点G落在BC边上时;③当点F落在AB边上时;④当点G落在AC边上时;进行讨论可得所有满足条件的n的值.
;再分四种情况:①当点F落在BC边上时;②当点G落在BC边上时;③当点F落在AB边上时;④当点G落在AC边上时;进行讨论可得所有满足条件的n的值.
试题解析:解:(1)∵点D(m,4)在直线AC上;
∴4=![]() m+8,解得m=﹣3,∴点D的坐标为(﹣3,4);
m+8,解得m=﹣3,∴点D的坐标为(﹣3,4);
(2)①如图1,过点D作DH⊥y轴于H,则EH=|n﹣4|
∴S=DE2=EH2+DH2=(n﹣4)2+9;
②当DF∥x轴时,点H即为正方形DEFG的中心,∴EH=DH=3,∴n=4+3=7,∴S=(7﹣4)2+9=18;
(3)∵OB=2OC=16,∴B为(16,0),∴BC为: ![]() ;
;
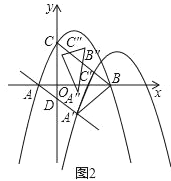
①当点F落在BC边上时,如图2,作DM⊥y轴于M,FN⊥y轴于N.在△DEM与△EFN中,  ,∴△DEM≌△EFN(AAS),∴NF=EM=n﹣4,EN=DM=3
,∴△DEM≌△EFN(AAS),∴NF=EM=n﹣4,EN=DM=3
∴F为(n﹣4,n﹣3)
∴n﹣3=﹣![]() (n﹣4)+8,∴n=
(n﹣4)+8,∴n=![]() ;
;
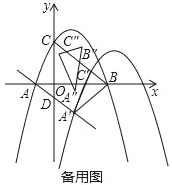
②当点G落在BC边上时,如图3,作DM⊥y轴于M,GN⊥DM轴于N,由①同理可得△DEM≌△GDN,∴GN=DM=3,DN=EM=n﹣4,∴点G纵坐标为1,∴![]() ,∴x=14,∴DN=14+3=17=n﹣4,∴n=21;
,∴x=14,∴DN=14+3=17=n﹣4,∴n=21;
③当点F落在AB边上时,如图4,作DM⊥y轴于M,由①同理可得△DEM≌△EFO,∴OE=DM=3,即n=3;
④当点G落在AC边上时,如图5.∵∠CDE=∠AOC=90°,∠DCE=∠OCA,∴△DCE∽△OCA,∴![]() ,∴
,∴![]() ,∴n=
,∴n=![]() ,显然,点G不落在AB边上,点F不落在AC边上,故只存在以上四种情况.
,显然,点G不落在AB边上,点F不落在AC边上,故只存在以上四种情况.
综上可得,当n=![]() 或21或3或
或21或3或![]() 时,正方形的顶点F或G落在△ABC的边上.
时,正方形的顶点F或G落在△ABC的边上.

 名校课堂系列答案
名校课堂系列答案