题目内容
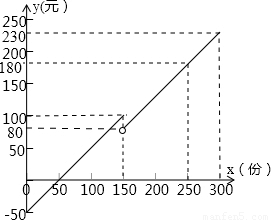
某早餐店每天的利润y(元)与售出的早餐x(份)之间的函数关系如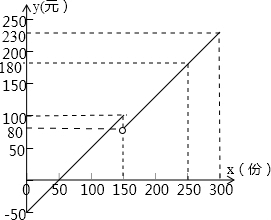 图所示.当每天售出的早餐超过150份时,需要增加一名工人.
图所示.当每天售出的早餐超过150份时,需要增加一名工人.
(1)该店每天至少要售出份早餐才不亏本;
(2)求出150<x≤300时,y关于x的函数解析式;
(3)要使每天有120元以上的盈利,至少要售出多少份早餐?
(4)该店每出售一份早餐,盈利多少元?
解:(1)当y=0时,x=50.
(2)设函数的解析式为y=kx+b,由题意得 .解方程组得
.解方程组得 .
.
所以函数的解析式为y=x-70.
(3)解不等式x-70>120,得x>190.
因此,至少要售出190份早餐,才能使每天有120元以上的盈利.
(4)∵(230-180)÷(300-250)=1,
∴该店每出售一份早餐,盈利1元.
分析:(1)直接根据图示可知每天至少要售出50份早餐才不亏本;
(2)利用待定系数法求解即可;
(3)利用“每天有120元以上的盈利”作为不等关系列不等式求解即可;
(4)根据图示可知(300-250)÷(230-180)=1.所以该店每出售一份早餐,盈利1元.
点评:主要考查利用一次函数的模型解决实际问题的能力和读图能力.要先根据题意列出函数关系式,再代数求值.解题的关键是要分析题意根据实际意义准确的列出解析式,再把对应值代入求解,并会根据图示得出所需要的信息.
(2)设函数的解析式为y=kx+b,由题意得
 .解方程组得
.解方程组得 .
.所以函数的解析式为y=x-70.
(3)解不等式x-70>120,得x>190.
因此,至少要售出190份早餐,才能使每天有120元以上的盈利.
(4)∵(230-180)÷(300-250)=1,
∴该店每出售一份早餐,盈利1元.
分析:(1)直接根据图示可知每天至少要售出50份早餐才不亏本;
(2)利用待定系数法求解即可;
(3)利用“每天有120元以上的盈利”作为不等关系列不等式求解即可;
(4)根据图示可知(300-250)÷(230-180)=1.所以该店每出售一份早餐,盈利1元.
点评:主要考查利用一次函数的模型解决实际问题的能力和读图能力.要先根据题意列出函数关系式,再代数求值.解题的关键是要分析题意根据实际意义准确的列出解析式,再把对应值代入求解,并会根据图示得出所需要的信息.

练习册系列答案
相关题目
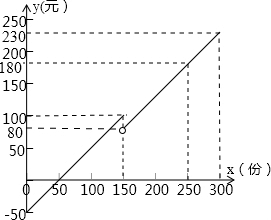 图所示.当每天售出的早餐超过150份时,需要增加一名工人.
图所示.当每天售出的早餐超过150份时,需要增加一名工人.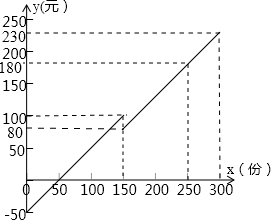 如图所示.当每天售出的早餐超过150份时,需要增加一名工人.
如图所示.当每天售出的早餐超过150份时,需要增加一名工人. 17、某早餐店每天的利润y(元)与售出的早餐x(份)之间的函数关系如图所示.当每天售出的早餐超过150份时,需要增加一名工人.该店每天至少要售出
17、某早餐店每天的利润y(元)与售出的早餐x(份)之间的函数关系如图所示.当每天售出的早餐超过150份时,需要增加一名工人.该店每天至少要售出 如图所示.当每天售出的早餐超过150份时,需要增加一名工人.
如图所示.当每天售出的早餐超过150份时,需要增加一名工人.