题目内容
我国古代数学家秦九韶在《数书九章》中记述了“三斜求积术”,即已知三角形的三边长,求它的面积.用现代式子表示即为: …①(其中a、b、c为三角形的三边长,s为面积).
…①(其中a、b、c为三角形的三边长,s为面积).而另一个文明古国古希腊也有求三角形面积的海伦公式:
s=
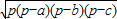 …②(其中p=
…②(其中p= .)
.)(1)若已知三角形的三边长分别为5,7,8,试分别运用公式①和公式②,计算该三角形的面积s;
(2)你能否由公式①推导出公式②?请试试.
【答案】分析:(1)代入计算即可;
(2)需要在括号内都乘以4,括号外再乘 ,保持等式不变,构成完全平方公式,再进行计算.
,保持等式不变,构成完全平方公式,再进行计算.
解答:解:(1)S= ,
,
=
 ;
;
P= (5+7+8)=10,
(5+7+8)=10,
又S=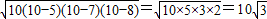 ;
;
(2) =
= (
( -
-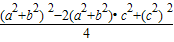 )
)
= ,
,
=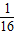 (c+a-b)(c-a+b)(a+b+c)(a+b-c),
(c+a-b)(c-a+b)(a+b+c)(a+b-c),
=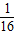 (2p-2a)(2p-2b)•2P•(2p-2c),
(2p-2a)(2p-2b)•2P•(2p-2c),
=p(p-a)(p-b)(p-c),
∴ =
= .
.
(说明:若在整个推导过程中,始终带根号运算当然也正确)
点评:考查了三角形面积的海伦公式的用法,也培养了学生的推理和计算能力.
(2)需要在括号内都乘以4,括号外再乘
 ,保持等式不变,构成完全平方公式,再进行计算.
,保持等式不变,构成完全平方公式,再进行计算.解答:解:(1)S=
 ,
,=

 ;
;P=
 (5+7+8)=10,
(5+7+8)=10,又S=
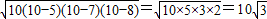 ;
;(2)
 =
= (
( -
-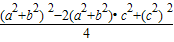 )
)=
 ,
,=
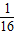 (c+a-b)(c-a+b)(a+b+c)(a+b-c),
(c+a-b)(c-a+b)(a+b+c)(a+b-c),=
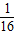 (2p-2a)(2p-2b)•2P•(2p-2c),
(2p-2a)(2p-2b)•2P•(2p-2c),=p(p-a)(p-b)(p-c),
∴
 =
= .
.(说明:若在整个推导过程中,始终带根号运算当然也正确)
点评:考查了三角形面积的海伦公式的用法,也培养了学生的推理和计算能力.

练习册系列答案
相关题目
 ……①(其中
……①(其中 、
、 、
、 为三角形的三边长,
为三角形的三边长, 为面积).
为面积).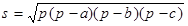 ……②(其中
……②(其中 ).
). ……①(其中
……①(其中 、
、 、
、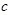 为三角形的三边长,
为三角形的三边长, 为面积).
为面积). ……②(其中
……②(其中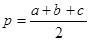 ).
). …①(其中a、b、c为三角形的三边长,s为面积).
…①(其中a、b、c为三角形的三边长,s为面积). …②(其中p=
…②(其中p= .)
.)