题目内容
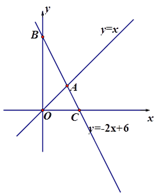
【题目】如图,直线![]() 与x轴、
与x轴、![]() 轴分别相交于点C、B,与直线
轴分别相交于点C、B,与直线![]() 相交于
相交于
点A.
(1)点B、点C和点A的坐标分别是(0, )、( ,0)、( , );
(2)求两条直线与![]() 轴围成的三角形的面积;
轴围成的三角形的面积;
(3)在坐标轴上是否存在一点Q,使△OAQ的面积等于6,若存在请直接写出Q点的坐标,若不存在,请说明理由.
【答案】(1) 6,3,2,2;(2)3;(3)存在,理由见解析.
【解析】分析:(1)根据坐标轴上点的坐标特征易得B点坐标为(0,6),C点坐标为(3,0),然后解方程组![]() 可确定A点坐标;(2)根据三角形面积公式计算;(3)分类讨论:当Q点在x轴上,设Q(a,0),则S△AOQ=
可确定A点坐标;(2)根据三角形面积公式计算;(3)分类讨论:当Q点在x轴上,设Q(a,0),则S△AOQ=![]() ×2×|a|=6;当Q点在y轴上,设Q(0,b),则S△AOQ=
×2×|a|=6;当Q点在y轴上,设Q(0,b),则S△AOQ=![]() ×2×|b|=6,然后分别求出a和b的值,从而得到Q点的坐标.
×2×|b|=6,然后分别求出a和b的值,从而得到Q点的坐标.
本题解析:
(1)把x=0代入y=2x+6得y=6,所以B点坐标为(0,6),
把y=0代入y=2x+6得2x+6=0,解得x=3,所以C点坐标为(3,0),
解方程组![]() 得
得![]() ,所以A点坐标为(2,2),
,所以A点坐标为(2,2),
故答案为6,3,2,2;
(2) ![]() =
=![]() ×3×2=3;
×3×2=3;
(3)存在。
当Q点在x轴上,设Q(a,0),则S△AOQ=![]() ×2×|a|=6,
×2×|a|=6,
解得a=±6,
则Q点坐标为(6,0)、(6,0);
当Q点在y轴上,设Q(0,b),则![]() =
=![]() ×2×|b|=6,
×2×|b|=6,
解得b=±6,
则Q点坐标为(0,6)、(0,6),
综上所述Q点坐标为(0,6)、(0,6)、(6,0)、(6,0).

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目