题目内容
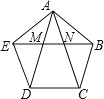
【题目】如图,在正五边形ABCDE中,对角线AD,AC与EB分别交于点M,N,则下列结论正确的是( )
A.EM:AE=2:(![]() -1)
-1)
B.MN:EM=(![]() -1):(3-
-1):(3-![]() )
)
C.AM:MN=(3-![]() ):(
):(![]() -1)
-1)
D.MN:DC=(3-![]() ):2
):2
【答案】D
【解析】
试题分析:根据正五边形的性质得到∠DAE=∠DAE,∠ADE=∠AEM=36°,推出△AME∽△AED,根据相似三角形的性质得到,得到AE2=ADAM,等量代换即可得到论.
∵五边形ABCDE是正五边形, ∴DE=AE=AB,∠AED=∠EAB=108°, ∴∠ADE=∠AEM=36°,
∴△AME∽△AED, ∴![]() , ∴AE2=ADAM, ∵AE=DE=DM, ∴DM2=ADAM,
, ∴AE2=ADAM, ∵AE=DE=DM, ∴DM2=ADAM,
设AE=DE=DM=2, ∴22=AM(AM+2), ∴AM=![]() ﹣1,(负值设去), ∴EM=BN=AM=
﹣1,(负值设去), ∴EM=BN=AM=![]() ﹣1,AD=
﹣1,AD=![]() +1, ∵BE=AD, ∴MN=BE﹣ME﹣BN=3﹣
+1, ∵BE=AD, ∴MN=BE﹣ME﹣BN=3﹣![]() , ∴MN:CD=(3-
, ∴MN:CD=(3-![]() ):2
):2

练习册系列答案
相关题目