题目内容
如图,已知一次函数y=-| 3 | 4 |
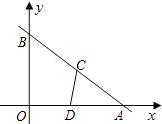 每秒1个单位的速度从点B向点A运动,同时点D在线段AO上以同样的速度从点A向点O运动,运动时间用t(单位:秒)表示.
每秒1个单位的速度从点B向点A运动,同时点D在线段AO上以同样的速度从点A向点O运动,运动时间用t(单位:秒)表示.(1)求AB的长;
(2)当t为何值时,△ACD与△AOB相似并直接写出此时点C的坐标;
(3)△ACD的面积是否有最大值?若有,此时t为何值;若没有,请说明理由.
分析:(1)首先容易求出A,B两点的坐标,然后求出OA,OB的长度,再利用勾股定理求AB;
(2)先用t分别表示AC,AD的长度,再根据相似的性质可以列出关于t的方程,解方程就可以求出点C的坐标;
(3)用t表示△ACD的面积,然后利用二次函数求最大值.
(2)先用t分别表示AC,AD的长度,再根据相似的性质可以列出关于t的方程,解方程就可以求出点C的坐标;
(3)用t表示△ACD的面积,然后利用二次函数求最大值.
解答:解:(1)当x=0时,y=3;当y=0时,x=4;
∴A(4,0),B(0,3),
∴OA=4,OB=3,
∴AB=
=5;
(2)依题意BC=t,AC=5-t,AD=t,
若△ACD∽△ABO,
∴
=
,
代入得:
=
,
解得:t=
,
若△ACD∽△AOB,
=
,
=
,
解得t=
,
故C(
,
)或(
,
);
(3)∵AC=5-t,AD=t,而sinA=
=
,
∴AD边上的高=
(5-t),
∴S△ACD=
×AD×
(5-t)=
(5t-t2),
∴S△ACD有最大值,此时t=2.5,
∵S△ACD=
(5t-t2)=-
(t-2.5)2+
,
∴当t=2.5时,S△ACD有最大值.
∴A(4,0),B(0,3),
∴OA=4,OB=3,
∴AB=
| 32+42 |
(2)依题意BC=t,AC=5-t,AD=t,
若△ACD∽△ABO,
∴
| AC |
| AB |
| AD |
| AO |
代入得:
| 5-t |
| 5 |
| t |
| 4 |
解得:t=
| 20 |
| 9 |
若△ACD∽△AOB,
| AD |
| AB |
| AC |
| AO |
| t |
| 5 |
| 5-t |
| 4 |
解得t=
| 25 |
| 9 |
故C(
| 25 |
| 9 |
| 11 |
| 12 |
| 20 |
| 9 |
| 4 |
| 3 |
(3)∵AC=5-t,AD=t,而sinA=
| OB |
| AB |
| 3 |
| 5 |
∴AD边上的高=
| 3 |
| 5 |
∴S△ACD=
| 1 |
| 2 |
| 3 |
| 5 |
| 3 |
| 10 |
∴S△ACD有最大值,此时t=2.5,
∵S△ACD=
| 3 |
| 10 |
| 3 |
| 10 |
| 15 |
| 8 |
∴当t=2.5时,S△ACD有最大值.
点评:此题既考查了勾股定理的计算,也考查了相似三角形的性质,还有利用二次函数求最大值.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
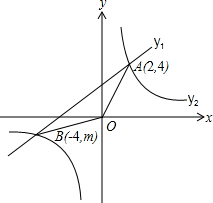 B(-4,m)两点.
B(-4,m)两点. 如图,已知一次函数y=kx+b的图象与反比例函数y=-
如图,已知一次函数y=kx+b的图象与反比例函数y=- (2013•新疆)如图,已知一次函数y1=kx+b与反比例函数
(2013•新疆)如图,已知一次函数y1=kx+b与反比例函数 如图,已知一次函数y=k1x+b经过A、B两点,将点A向上平移1个单位后刚好在反比例函数
如图,已知一次函数y=k1x+b经过A、B两点,将点A向上平移1个单位后刚好在反比例函数 如图,已知一次函数y=kx+b的图象交反比例函数
如图,已知一次函数y=kx+b的图象交反比例函数