题目内容
(2004•济宁)阅读下面材料:在计算1+4+7+10+13+16+19+22+25+28时,我们发现,从第一个数开始,以后的每个数与它的前一个数的差都是一个相同的定值,具有这种规律的一列数,求和时,除了直接相加外,我们还可以用公式
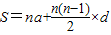 来计算(公式中的S表示它们的和,n表示数的个数,a表示第一个数的值,d表示这个相差的定值).那么S=1+4+7+10+13+16+19+22+25+28=
来计算(公式中的S表示它们的和,n表示数的个数,a表示第一个数的值,d表示这个相差的定值).那么S=1+4+7+10+13+16+19+22+25+28=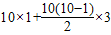 =145.
=145.用上面的知识解决下列问题:
我市某乡镇具有“中国北方乔木之乡”的美称,到2000年底这个镇已有苗木2万亩,为增加农民收入,这个镇实施“苗木兴镇”战略,逐年有计划地扩种苗木.从2001年起,以后每年又比上一年多种植相同面积的苗木;从2001年起每年卖出成苗木,以后每年又比上一年多卖出相同面积的苗木.下表为2001年、2002年、2003年三年种植苗木与卖出成苗木的面积统计数据.
| 年份 | 2001年 | 2002年 | 2003年 |
| 每年种植苗木的面积(亩) | 4000 | 5000 | 6000 |
| 每年卖出成苗木的面积(亩) | 2000 | 2500 | 3000 |
【答案】分析:设在2万亩的基础上过x年,这个镇的苗木面积达到5万亩.根据表格中的数据可以分析得到从2001年起,在2万亩的基础上,每一年的苗木面积增加2000亩,2500亩,3000亩…,2000+500(x-1).即可列方程求解.
解答:解:设在2万亩的基础上过x年,这个镇的苗木面积达到5万亩.
20000+2000+2500+…+2000+500(x-1)=50000,
2000x+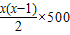 =30000,
=30000,
(x-8)(x+15)=0,
x1=8,x2=-15(负值舍去).
答:到2008年底,这个镇的苗木面积达到5万亩.
点评:此题能够根据表格正确找到规律,注意根据题目中提供的公式进行计算.
解答:解:设在2万亩的基础上过x年,这个镇的苗木面积达到5万亩.
20000+2000+2500+…+2000+500(x-1)=50000,
2000x+
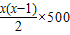 =30000,
=30000,(x-8)(x+15)=0,
x1=8,x2=-15(负值舍去).
答:到2008年底,这个镇的苗木面积达到5万亩.
点评:此题能够根据表格正确找到规律,注意根据题目中提供的公式进行计算.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案
相关题目
(2004•济宁)某市甲、乙两个汽车销售公司,去年一至十月份每月销售同种品牌汽车的情况如图所示:
(1)请你根据上图填写下表:
(2)请你从以下两个不同的方面对甲、乙两个汽车销售公司去年一至十月份的销售情况进行分析:
①从平均数和方差结合看;
②从折线图上甲、乙两个汽车销售公司销售数量的趋势看(分析哪个汽车销售公司较有潜力).

(1)请你根据上图填写下表:
| 销售公司 | 平均数 | 方差 | 中位数 | 众数 |
| 甲 | 5.2 | 9 | ||
| 乙 | 9 | 17.0 | 8 |
①从平均数和方差结合看;
②从折线图上甲、乙两个汽车销售公司销售数量的趋势看(分析哪个汽车销售公司较有潜力).

(2004•济宁)阅读下面材料:
在计算1+4+7+10+13+16+19+22+25+28时,我们发现,从第一个数开始,以后的每个数与它的前一个数的差都是一个相同的定值,具有这种规律的一列数,求和时,除了直接相加外,我们还可以用公式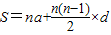 来计算(公式中的S表示它们的和,n表示数的个数,a表示第一个数的值,d表示这个相差的定值).那么S=1+4+7+10+13+16+19+22+25+28=
来计算(公式中的S表示它们的和,n表示数的个数,a表示第一个数的值,d表示这个相差的定值).那么S=1+4+7+10+13+16+19+22+25+28=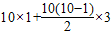 =145.
=145.
用上面的知识解决下列问题:
我市某乡镇具有“中国北方乔木之乡”的美称,到2000年底这个镇已有苗木2万亩,为增加农民收入,这个镇实施“苗木兴镇”战略,逐年有计划地扩种苗木.从2001年起,以后每年又比上一年多种植相同面积的苗木;从2001年起每年卖出成苗木,以后每年又比上一年多卖出相同面积的苗木.下表为2001年、2002年、2003年三年种植苗木与卖出成苗木的面积统计数据.
假设所有苗木的成活率都是100%,问到哪一年年底,这个镇的苗木面积达到5万亩?
在计算1+4+7+10+13+16+19+22+25+28时,我们发现,从第一个数开始,以后的每个数与它的前一个数的差都是一个相同的定值,具有这种规律的一列数,求和时,除了直接相加外,我们还可以用公式
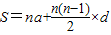 来计算(公式中的S表示它们的和,n表示数的个数,a表示第一个数的值,d表示这个相差的定值).那么S=1+4+7+10+13+16+19+22+25+28=
来计算(公式中的S表示它们的和,n表示数的个数,a表示第一个数的值,d表示这个相差的定值).那么S=1+4+7+10+13+16+19+22+25+28=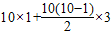 =145.
=145.用上面的知识解决下列问题:
我市某乡镇具有“中国北方乔木之乡”的美称,到2000年底这个镇已有苗木2万亩,为增加农民收入,这个镇实施“苗木兴镇”战略,逐年有计划地扩种苗木.从2001年起,以后每年又比上一年多种植相同面积的苗木;从2001年起每年卖出成苗木,以后每年又比上一年多卖出相同面积的苗木.下表为2001年、2002年、2003年三年种植苗木与卖出成苗木的面积统计数据.
| 年份 | 2001年 | 2002年 | 2003年 |
| 每年种植苗木的面积(亩) | 4000 | 5000 | 6000 |
| 每年卖出成苗木的面积(亩) | 2000 | 2500 | 3000 |
 ,在(2)的条件下,试判断是否存在m的值,使经过点C及抛物线与x轴的一个交点的⊙M与y轴的正半轴相切于点D,且被x轴截得的劣弧与
,在(2)的条件下,试判断是否存在m的值,使经过点C及抛物线与x轴的一个交点的⊙M与y轴的正半轴相切于点D,且被x轴截得的劣弧与 是等弧?若存在,求出所有满足条件的m的值;若不存在,说明理由.
是等弧?若存在,求出所有满足条件的m的值;若不存在,说明理由. ,在(2)的条件下,试判断是否存在m的值,使经过点C及抛物线与x轴的一个交点的⊙M与y轴的正半轴相切于点D,且被x轴截得的劣弧与
,在(2)的条件下,试判断是否存在m的值,使经过点C及抛物线与x轴的一个交点的⊙M与y轴的正半轴相切于点D,且被x轴截得的劣弧与 是等弧?若存在,求出所有满足条件的m的值;若不存在,说明理由.
是等弧?若存在,求出所有满足条件的m的值;若不存在,说明理由.