题目内容
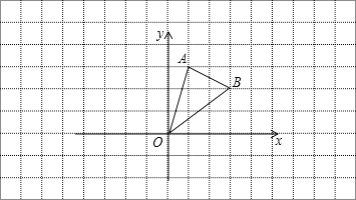
【题目】如图,直线l是一次函数y=kx+b的图象,点A、B在直线l上.根据图象回答下列问题:
(1)写出方程kx+b=0的解;
(2)写出不等式kx+b>1的解集;
(3)若直线l上的点P(m,n)在线段AB上移动,则m、n应如何取值.
【答案】
(1)解:函数与x轴的交点A坐标为(-2,0),与y轴的交点的坐标为(0,1),且y随x的增大而增大.
函数经过点(-2,0),则方程kx+b=0的根是x=-2
(2)解:函数经过点(0,1),则当x>0时,有kx+b>1,
即不等式kx+b>1的解集是x>0
(3)解:线段AB的自变量的取值范围是:-2≤x≤2,
当-2≤m≤2时,函数值y的范围是0≤y≤2,
则0≤n≤2
【解析】(1)观察函数图像可知直线AB与x轴交于点(-2,0),因此直线y=kx+b与x轴交点的横坐标就是方程kx+b=0的解,即可得出结果。
(2)根据图像可知直线AB与y轴交点坐标为(0,1),要使kx+b>1,就要观察y轴右侧的图像,就可求出x的取值范围。
(3)抓住已知条件点P(m,n)在线段AB上移动,根据点A、B的坐标就可得出m、n的取值范围。

练习册系列答案
相关题目