题目内容
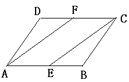18、已知：如图，在平行四边形ABCD中，E，F分别为AB，CD的中点．求证：（1）△AFD≌△CEB；
（2）四边形AECF是平行四边形．（选做一个结论；本题最多得7分）
分析：（1）平行四边形两组对边分别相等，对角相等，所以可根据边角边进行证明全等．
（2）在（1）的基础上，可利用一组对边平行且相等去证明．
（2）在（1）的基础上，可利用一组对边平行且相等去证明．
解答：解：（1）在?ABCD中，BC=DA，∠B=∠D，AB=CD，
又∵E，F分别为AB，CD的中点，
∴BE=DF．
∴△AFD≌△CEB．
（2）由（1）得，FC=AE，FC∥AE，
∴四边形AECF为平行四边形．
又∵E，F分别为AB，CD的中点，
∴BE=DF．
∴△AFD≌△CEB．
（2）由（1）得，FC=AE，FC∥AE，
∴四边形AECF为平行四边形．
点评：本题主要考查了平行四边形的性质以及判定，难易程度适中平行四边形的五种判定方法与平行四边形的性质相呼应，每种方法都对应着一种性质，在应用时应注意它们的区别与联系．
练习册系列答案
阅读快车系列答案
相关题目
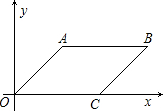如图，在平行四边形ABC0中，已知点A、C两点的坐标为A（
（2013•南平模拟）如图，已知四边形ABCD．请在下列四个关系中，选出两个恰当的关系作为条件，推出四边形ABCD是平行四边形，并予证明．
如图，在平行四边形OABC中，已知点A、C两点的坐标为A （
3，
，将∠OBA对折，使点O的对应点H恰好落在直线AB上，折痕交x轴于点C，