Question

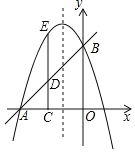
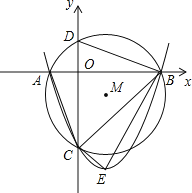
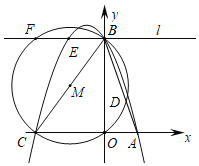
【题目】已知x轴上有点A（1，0），点B在y轴上，点C（m，0）为x轴上一动点且m＜﹣1，连接AB，BC，tan∠ABO，以线段BC为直径作⊙M交线段AB于点D，过点B作直线l∥AC过A，B，C三点的抛物线为y＝ax2+bx+e，直线与抛物线和⊙M的另一个交点分别是E，F，当EF＝BD时，则m的值为_____．

Answer 1

【答案】．

【解析】

先通过tan∠ABO及A（1，0）求出点B的坐标，然后将A,B,C代入抛物线的解析式中，求出相应的a,b,e,用含m的式子表示出抛物线的对称轴，利用抛物线的对称性，可得EB,FB的长，进而求出EF的长为定长；连接CD，证明△CAD∽△BAO，列出比例式，将相关线段代入，化简即可求出m的值.

∵A（1，0），

∴OA=1，

∵tan∠ABO，

∴OB＝2，即：点B的坐标为（0，2）．

点C（m，0），A（1，0），B（0，2）在抛物线y＝ax2+bx+e上，

∴，

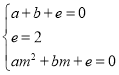解得：b，a，

∴对称轴x．

∵EB＝﹣（1+m），FB＝﹣m，EF＝FB﹣EB＝1，

∴线段EF的长是定值1．

∴BD＝EF＝1．

如图所示，连接CD

∵BC为直径

∴∠CDB＝90°

∴∠CDA＝∠AOB＝90°，∠CAD＝∠BAO

∴△CAD∽△BAO

∴

A（1，0），B（0，2），C（m，0），

∴AB，AC＝1﹣m，AO＝1

∵BD＝1

∴AD1

∴

∴1﹣m＝5

∴m

故答案为：．