题目内容
在做解方程练习时,学习卷中有一个方程“2y-| 1 |
| 2 |
| 1 |
| 2 |
分析:把x=2代入代数式5(x-1)-2(x-2)-4,求出“2y-
=
y+■”的y,再代入该式子求出■.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:当x=2时,代数式5(x-1)-2(x-2)-4
=5x-5-2x+4-4(4分)
=3x-5(6分)
=3×2-5=1(8分)
即y=1(9分)
代入方程中得到:2×1-
=
×1+■(10分)
解得■=1
即这个常数是1.(13分)
=5x-5-2x+4-4(4分)
=3x-5(6分)
=3×2-5=1(8分)
即y=1(9分)
代入方程中得到:2×1-
| 1 |
| 2 |
| 1 |
| 2 |
解得■=1
即这个常数是1.(13分)
点评:根据题意先求出y,将■看作未知数,把已知解代入方程的未知数中,使未知数转化为已知数,从而建立起未知系数的方程,通过未知系数的方程求出未知数系数,这种解题方法叫做待定系数法,是数学中的一个重要方法,以后在函数的学习中将大量用到这种方法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
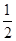 =
=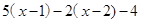 的值相同.”聪明的小聪很快补上了这个常数.同学们,你们能补上这个常数吗?
的值相同.”聪明的小聪很快补上了这个常数.同学们,你们能补上这个常数吗?