题目内容
【题目】如图，OM＝2，MN＝6，A为射线ON上的动点，以OA为一边作内角∠OAB＝120°的菱形OABC，则BM＋BN的最小值为 （ ）
A. 
B. 6 C. 
D. 
【答案】C
【解析】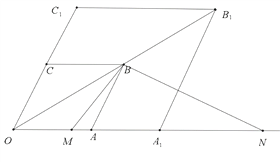
如图，连接OB，OB1，
∵菱形OABC，∠OAB=120°，∴∠OBA=30°，
同理可证，∠OB1A1=30°，
在四边形BAA1B1中，∠ABB1=360°－60°－30°－120°=150°，
∴∠OBA+∠ABB1=180°，
∴O、B、B1三点共线，
∴要求BM+BM最小，即要在射线OB1上找一点B使得B点到M、N点的距离之和最小，
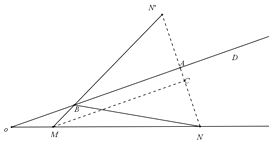
如图，作点N关于射线OD的对称点N＇,连接M N＇交射线OD于点B，此时BM+BN最小，作MC⊥NN＇交NN＇于点C，
∵OA⊥NN＇，∴MC∥OA，∴∠O=∠CMN=30°，
∵OM=2，MN=6，∴ON=8，∴AN=AN＇=4，CN=3，∴MC=3
，AC=1，∴CN＇=5，
∴BM+BN=BM+BN＇=M N＇,
（M N＇）2=（MC）2+（CN＇） 2=27+25=52，
∴M N＇=2
．
故选C．
练习册系列答案
举一反三期末百分冲刺卷系列答案
相关题目
