题目内容
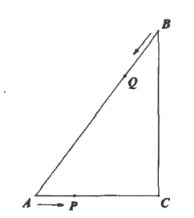
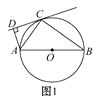
【题目】如图1,AB是☉O的直径,C为☉O上一点,直线CD与☉O相切于点C,AD⊥CD,垂足为D.
(1)求证:△ACD∽△ABC.
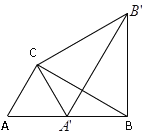
(2)如图2,将直线CD向下平移与☉O相交于点C,G,但其他条件不变.若AG=4,BG=3,求tan∠CAD的值.

【答案】(1)见解析;(2)![]()
【解析】试题分析:(1)连接OC,求出∠ADC=∠ACB,∠DCA=∠B,根据相似三角形的判定推出即可;
(2)根据圆内接四边形的性质求解即可.
试题解析:(1)如图,连接OC,
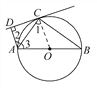
∵直线CD与☉O相切于C,∴OC⊥CD.
又∵AD⊥CD,∴AD∥OC,∴∠1=∠2.
∵OC=OA,∴∠1=∠3.∴∠2=∠3.
又∵AB为☉O的直径,∴∠ACB=90°.
∴∠ADC=∠ACB.
∴△ACD∽△ABC.
(2)∵四边形ABGC为☉O的内接四边形,
∴∠B+∠ACG=180°.
∵∠ACG+∠ACD=180°,∴∠ACD=∠B.
∵∠ADC=∠AGB=90°,∴∠DAC=∠GAB.
在Rt△ABG中,AG=4,BG=3,
∴tan∠GAB=![]() =
=![]() .
.
∴tan∠DAC=![]() .
.

练习册系列答案
相关题目