ЬтФПФкШн
ЁОЬтФПЁПШчЭМЃЌдкRtЁїBCDжаЃЌЁЯCBDЃН90ЁуЃЌBCЃНBDЃЌЕуAдкCBЕФбгГЄЯпЩЯЃЌЧвBAЃНBCЃЌЕуEдкжБЯпBDЩЯвЦЖЏЃЌЙ§ЕуEзїЩфЯпEFЁЭEAЃЌНЛCDЫљдкжБЯпгкЕуFЃЎ

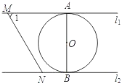
ЃЈ1ЃЉЪдЧѓжЄЭМЃЈ1ЃЉжаЃКЁЯBAEЃНЁЯDEFЃЛ
ЃЈ2ЃЉЕБЕуEдкЯпЖЮBDЩЯвЦЖЏЪБЃЌШчЭМЃЈ1ЃЉЫљЪОЃЌЧѓжЄЃКAEЃНEFЃЛ
ЃЈ3ЃЉЕБЕуEдкжБЯпBDЩЯвЦЖЏЪБЃЌдкЭМЃЈ2ЃЉгыЭМЃЈ3ЃЉжаЃЌЗжБ№ВТЯыЯпЖЮAEгыEFгадѕбљЕФЪ§СПЙиЯЕЃЌВЂОЭЭМЃЈ3ЃЉЕФВТЯыНсЙћЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉМћНтЮіЃЛЃЈ2ЃЉМћНтЮіЃЛЃЈ3ЃЉAEЃНEFЃЌРэгЩМћНтЮі.
ЁОНтЮіЁП
(1)гЩЁЯAEB+ЁЯAЃН90ЁуКЭЁЯAEB+ЁЯFEDЃН90ЁуМДПЩЕУЕННсТл.
(2)ШчЭМ1жаЃЌдкBAЩЯНиШЁBHЃЌЪЙЕУBH=BE.ЙЙдьШЋЕШШ§НЧаЮМДПЩНтОіЮЪЬтЃЛ
(3)ШчЭМ2жаЃЌдкBCЩЯНиШЁBH=BEЃЌЭЌЗЈПЩжЄЃЛШчЭМ3жаЃЌдкBAЩЯНиШЁBHЃЌЪЙЕУBH=BE.ЭЌЗЈПЩжЄ.
ЃЈ1ЃЉжЄУїЃКЁпдкRtЁїBCDжаЃЌЁЯCBDЃН90ЁуЃЌЕуAдкCBЕФбгГЄЯпЩЯЃЌ
ЁрЁЯABDЃН90ЁуЃЌ
ЁрЁЯAEB+ЁЯAЃН90ЁуЃЌ
ЁпEFЁЭEAЃЌ
ЁрЁЯAEB+ЁЯFEDЃН90ЁуЃЌ
ЁрЁЯBAEЃНЁЯDEFЃЛ
ЃЈ2ЃЉжЄУїЃКШчЭМ1жаЃЌдкBAЩЯНиШЁBHЃЌЪЙЕУBHЃНBEЃЎ

ЁпBCЃНABЃНBDЃЌBEЃНBHЃЌ
ЁрAHЃНEDЃЌ
ЁпЁЯAEFЃНЁЯABEЃН90ЁуЃЌ
ЁрЁЯAEB+ЁЯFEDЃН90ЁуЃЌЁЯAEB+ЁЯBAEЃН90ЁуЃЌ
ЁрЁЯFEDЃНЁЯHAEЃЌ
ЁпЁЯBHEЃНЁЯCDBЃН45ЁуЃЌ
ЁрЁЯAHEЃНЁЯEDFЃН135ЁуЃЌ
ЁрЁїAHEЁеЁїEDFЃЈAASЃЉЃЌ
ЁрAEЃНEFЃЎ
ЃЈ3ЃЉНтЃКШчЭМ2жаЃЌдкBCЩЯНиШЁBHЃНBEЃЌЭЌЗЈПЩжЄЃКAEЃНEFЃЌ
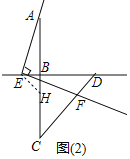
ШчЭМ3жаЃЌбгГЄBAжСЕуHЃЌЪЙЕУBHЃНBEЃЎЭЌЗЈПЩжЄЃКAEЃНEFЃЎ