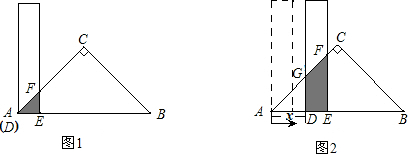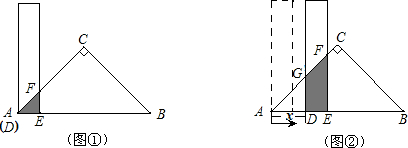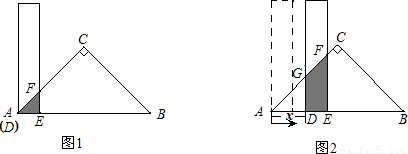Question

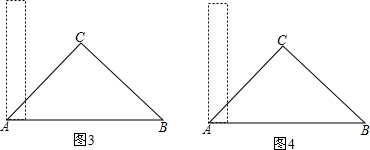
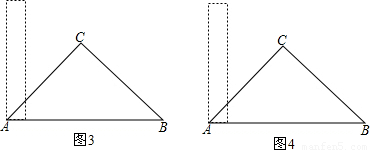
有一根直尺的短边长2cm，长边长10cm，还有一块锐角为45°的直角三角形纸板，其中直角三角形纸板的斜边长为12cm．按图-1的方式将直尺的短边DE放置在与直角三角形纸板的斜边AB上，且点D与点A重合．若直尺沿射线AB方向平行移动，如图-2，设平移的长度为x（cm），直尺和三角形纸板的重叠部分（图中阴影部分）的面积为S （cm²）．
（1）当x=0时，S=

 

；当x=10时，S=

 

；
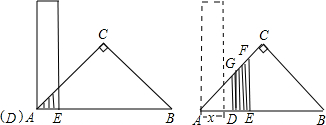
（2）当0＜x≤4时，如图-2，求S与x的函数关系式；
（3）当6＜x＜10时，求S与x的函数关系式；
（4）请你作出推测：当x为何值时，阴影部分的面积最大？并写出最大值．

Answer 1

分析：本题考查二次函数的应用，根据移动的距离和三角形的性质进行计算，关键是要进行分段计算，把每段算好后再进行总结．

解答：解：（1）由题意可知：
当x=0时，△ABC是等腰直角三角形，
此时AE=EF=2，
则阴影部分的面积为S=

1

2

×2×2=2；
故答案为：2；
当x=10时，直尺运动到最右边，
阴影部分的面积为：S=

1

2

×2×2=2；
故答案为：2；

（2）当0＜x≤4时，阴影部分的面积为：S=

1

2

×（x+2）×（x+2）-

1

2

x²=2x+2；

（3）当6＜x＜10时，由分析可知：阴影部分的面积为：
S=

1

2

×（12-x）（12-x）-

1

2

×（12-x-2）×（12-x-2）
=

1

2

×（12-x）（12-x）-

1

2

×（10-x）×（10-x）
=-2x+22；

（4）当4≤x≤6时，可得S=-x²+10x-14；
所以S=

2x+2       0＜x≤4 - x2+10x-14   4≤x≤6 -2x+22       6＜x＜10

则：当x=5时，S有最大值=11．

点评：本题考查的是二次函数在实际生活中的应用，比较简单．同时还有三角形的面积及不规则图形的面积计算．