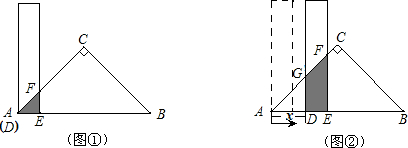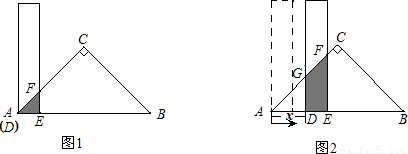题目内容
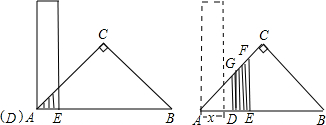
有一根直尺的短边长2cm,长边长10cm,还有一块锐角为45°的直角三角形纸板,它的斜边长12cm.如图1,将直尺的短边DE放置与直角三角形纸板的斜边AB重合,且点D与点A重合.将直尺沿AB方向平移(如图2),设平移的长度为xcm(0≤x≤10),直尺和三角形纸板的重叠部分(图中阴影部分)的面积为Scm2.(1)当x=0时(如图1),S=
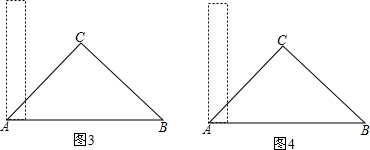
(2)当0<x≤4时(如图2),求S关于x的函数关系式;
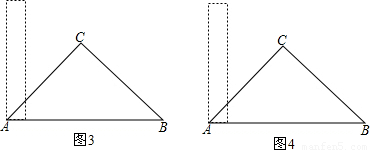
(3)当4<x<10时,求S关于x的函数关系式,并求出S的最大值(同学可在图3、图4中画草图).
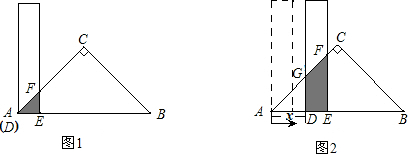
分析:(1)当x=0时,重合部分是等腰直角三角形AEF,因此面积为
×2×2=2.
当x=10时,E与B重合,此时重合部分是等腰直角三角形BDG,面积与x=0时相同.
(2)当0<x≤4时,F在AC上运动(包括与C重合).重合部分是直角梯形DEFG,易知:三角形ADG和AEF均为等腰直角三角形,因此DG=x,EF=x+2,可根据梯形的面积公式求出此时S,x的函数关系式.
(3)当4<x<10时,F在BC上运动(与B、C不重合).要分类讨论:
①当G在AC上,F在BC上运动时,即当4<x<6时,重合部分是五边形CGDEF,可用三个等腰直角三角形ABC,ADG,BEF的面积差来求得.
②当G、F同在BC上运动时(包括G、C重合),即当6≤x<10时,解法同(2).
根据上述两种情况可得出两个关于S,x的函数关系式,根据函数的性质和各自的自变量的取值范围即可求出S的最大值及对应的x的值.
| 1 |
| 2 |
当x=10时,E与B重合,此时重合部分是等腰直角三角形BDG,面积与x=0时相同.
(2)当0<x≤4时,F在AC上运动(包括与C重合).重合部分是直角梯形DEFG,易知:三角形ADG和AEF均为等腰直角三角形,因此DG=x,EF=x+2,可根据梯形的面积公式求出此时S,x的函数关系式.
(3)当4<x<10时,F在BC上运动(与B、C不重合).要分类讨论:
①当G在AC上,F在BC上运动时,即当4<x<6时,重合部分是五边形CGDEF,可用三个等腰直角三角形ABC,ADG,BEF的面积差来求得.
②当G、F同在BC上运动时(包括G、C重合),即当6≤x<10时,解法同(2).
根据上述两种情况可得出两个关于S,x的函数关系式,根据函数的性质和各自的自变量的取值范围即可求出S的最大值及对应的x的值.
解答:解:(1)2;2
(2)在Rt△ADG中,∠A=45°,
∴DG=AD=x,同理EF=AE=x+2,
∴S梯形DEFG=
(x+x+2)×2=2x+2.
∴S=2x+2
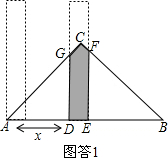
(3)①当4<x<6时(如图答1)
 ,
,
GD=AD=x,EF=EB=12-(x+2)=10-x,
则S△ADG=
AD•DG=
x2,S△BEF=
(10-x)2,
而S△ABC=
×12×6=36,S△BEF=
(10-x)2,
∴S=36-
x2-
(10-x)2=-x2+10x-14,
S=-x2+10x-14=-(x-5)2+11,
∴当x=5,(4<x<6)时,S最大值=11.
②当6≤x<10时(如图答2),
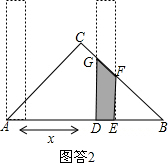
BD=DG=12-x,BE=EF=10-x,S=
(12-x+10-x)×2=22-2x.
S随x的增大而减小,所以S≤10.
由①、②可得,当4<x<10时,S最大值=11.
(2)在Rt△ADG中,∠A=45°,
∴DG=AD=x,同理EF=AE=x+2,
∴S梯形DEFG=
| 1 |
| 2 |
∴S=2x+2
(3)①当4<x<6时(如图答1)
 ,
,GD=AD=x,EF=EB=12-(x+2)=10-x,
则S△ADG=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
而S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
∴S=36-
| 1 |
| 2 |
| 1 |
| 2 |
S=-x2+10x-14=-(x-5)2+11,
∴当x=5,(4<x<6)时,S最大值=11.
②当6≤x<10时(如图答2),

BD=DG=12-x,BE=EF=10-x,S=
| 1 |
| 2 |
S随x的增大而减小,所以S≤10.
由①、②可得,当4<x<10时,S最大值=11.
点评:本题是运动性问题,考查了等腰直角三角形的性质,矩形的性质、图形面积的求法及二次函数的综合应用等知识.

练习册系列答案
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案
相关题目