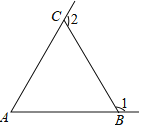
��Ŀ����
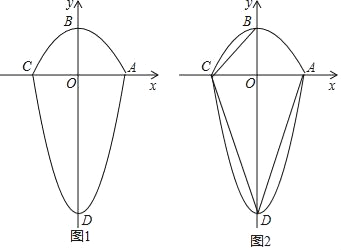
����Ŀ�����֣�1����ͼ1���ѡ�ABC��DE�۵���ʹ��A���ڵ�A�����������жϡ�1+��2���A�к�������ϵ��ֱ��д����Ľ��ۣ�����˵������
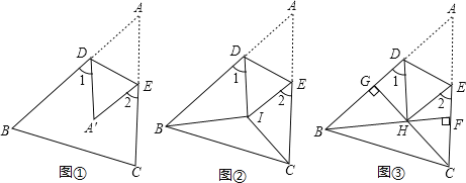
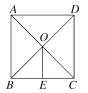
˼����2����ͼ2��BIƽ�֡�ABC��CIƽ�֡�ACB���ѡ�ABC�۵���ʹ��A���I�غϣ�����1+��2=100�㣬���BIC�Ķ�����
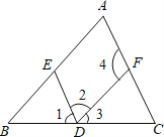
��չ��3����ͼ3������ǡ�ABC�У�BF��AC�ڵ�F��CG��AB�ڵ�G��BF��CG���ڵ�H���ѡ�ABC�۵�ʹ��A�͵�H�غϣ���̽����BHC���1+��2�Ĺ�ϵ����֤����Ľ��ۣ�
���𰸡���1����1+��2=2��A�����ɼ���������2����BIC=115�㣻��3����BHC=180��-![]() ����1+��2����
����1+��2����
��������
��1�����ݷ��۱任�����ʡ��������ڽǺͶ������Լ�ƽ�ǵĶ���������ɣ�
��2�����������ν�ƽ���ߵ����ʵó���IBC+��ICB=90��-![]() ��A�����������ε��ڽǺͶ������������BIC�Ķ����ɣ�
��A�����������ε��ڽǺͶ������������BIC�Ķ����ɣ�
��3�����ݴ��ߵ����ʵó�����AFH+��AGH=90��+90��=180�����������ı���AGHF���ڽǺ�Ϊ360�㣬��ʾ��![]() ��
��![]() �Ĺ�ϵ�����öԶ��ǵ����������õ�
�Ĺ�ϵ�����öԶ��ǵ����������õ�![]() ��
��![]() �Ĺ�ϵ���ٽ�ϵڣ�1���ʣ��õ���BHC���1+��2�Ĺ�ϵ��
�Ĺ�ϵ���ٽ�ϵڣ�1���ʣ��õ���BHC���1+��2�Ĺ�ϵ��
�⣺��1����1+��2=2��A��
���ɣ����ݷ��۵����ʣ���ADE=![]() ��180��-��1������AED=
��180��-��1������AED=![]() ��180��-��2����
��180��-��2����
�ߡ�A+��ADE+��AED=180�㣬
���A+![]() ��180-��1��+
��180-��1��+![]() ��180-��2��=180�㣬
��180-��2��=180�㣬
������2��A=��1+��2��
��2��![]() �ɣ�1��֪����1+��2=2��A��
�ɣ�1��֪����1+��2=2��A��
��![]() ��1+��2=100�㣬
��1+��2=100�㣬
���A=50��
��IBƽ�֡�ABC��ICƽ�֡�ACB��
���IBC+��ICB=![]() ����ABC+��ACB��=
����ABC+��ACB��=![]() ��180��-��A��=90��-
��180��-��A��=90��-![]() ��A��
��A��
���BIC=180��-����IBC+��ICB��=180��-��90��-![]() ��A��=90��+
��A��=90��+![]() ��A=90��+
��A=90��+![]() ��50��=115�㣻
��50��=115�㣻
��3����BF��AC��CG��AB��
���AFH+��AGH=90��+90��=180�㣬
���FHG+��A=180�㣬
���BHC=��FHG=180��-��A��
�ɣ�1��֪��1+��2=2��A��
���A=![]() ����1+��2����
����1+��2����
���BHC=180��-![]() ����1+��2����
����1+��2����