Question

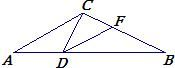
已知：如图，在△ABC中，D是AB边上的一点，BD＞AD，∠A=∠ACD，
（1）若AC=BC，△ACD的周长是7厘米，且

CD

CB

=

2

3

，求AB的长；
（2）过D作∠CDB的平分线DF交CB于F，若线段AC沿着AB方向平移，当点A移到点D时，判断线段AC的中点E能否移到线段DF上，并说明理由．

Answer 1

（1）∵

CD

CB

=

2

3

，AC=CB，∴AC=

3

2

CD，
又∵∠A=∠ACD，∴AD=DC，
由△ACD的周长是7厘米，可解得AD=DC=2cm，AC=3cm，
∵AC=CB，∴∠A=∠B，∴∠ADC=∠ACB，
△ACB∽△ADC，
∴

AC

AB

=

AD

BC

，解得AB=4.5cm．

（2）∵DF是∠CDB的平分线，∴∠CDF=∠BDF，
又∵∠CDB=∠A+∠ACD，∠A=∠ACD，
∴∠CDB=2∠A=2∠BDF，
∴∠A=∠BDF，
∴DF∥AC，
∴线段AC沿着AB方向平移，当点A移到点D时，线段AC的中点E能移到线段DF上．