题目内容
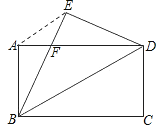
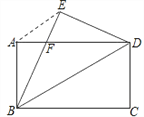
【题目】如图,将矩形纸片ABCD沿对角线BD折叠,点C落在点E处,BE交AD于点F,连接AE.
求证:(1)BF=DF;
(2)AE∥BD;
(3)若AB=6,AD=8,求BF的长.
【答案】(1)证明见解析;(2)证明见解析;(3)BF的长为 ![]() .
.
【解析】试题分析:(1)由矩形的性质和折叠的性质可得到∠ADB=∠EBD,从而得BF=DF;
(2)根据矩形的性质和三角形内角可得∠AEB=∠FBD,再根据平行线的判定即可得;
(3)在Rt△ABF中 ,设BF=FD=![]() ,则AF
,则AF ![]() ,利用勾股定理即可得.
,利用勾股定理即可得.
试题解析:(1)在矩形ABCD中,AD∥BC,AD=BC,∴ ∠DBC=∠ADB,
∵ ∠DBC=∠EBD ,∴ ∠ADB=∠EBD,∴ BF=FD;
(2)∵ AD=BC=BE ,BF=DF ,∴ AF=EF,∴ ∠AEB=∠EAF,
∵ ∠AFE=∠BFD ,∠FBD=∠FDB,∴ ∠AEB=∠EBD, ∴ AE∥BD;
(3)在Rt△ABF中 ,设BF=FD=![]() ,则AF
,则AF ![]() ,则
,则
![]() ,解得:
,解得: ![]() , ∴ BF的长为
, ∴ BF的长为 ![]() .
.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目