题目内容
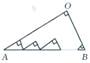
【题目】如图所示,已知MN⊥PQ于点O,点A、 ![]() 是以MN为轴的对称点,而点
是以MN为轴的对称点,而点 ![]() 、A是以PQ为轴的对称点,求证:点
、A是以PQ为轴的对称点,求证:点 ![]() 、
、 ![]() 是以点O为对称中心的对称点.
是以点O为对称中心的对称点.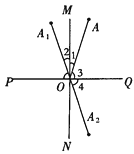
【答案】证明:∵点A、 ![]() 关于MN轴对称,∴OA=
关于MN轴对称,∴OA= ![]() ,∠1=∠2,同理OA=
,∠1=∠2,同理OA= ![]() ,∠3=∠4,∴
,∠3=∠4,∴ ![]() =
= ![]() ,∠1+∠2+∠3+∠4=2(∠1+∠3)=180°,∴点
,∠1+∠2+∠3+∠4=2(∠1+∠3)=180°,∴点 ![]() 、
、 ![]() 是以点O为对称中心的对称点.
是以点O为对称中心的对称点.
【解析】中心对称的性质:对称点所连线段都经过对称中心,而且被对称中心所平分.
【考点精析】本题主要考查了中心对称及中心对称图形的相关知识点,需要掌握如果把一个图形绕着某一点旋转180度后能与另一个图形重合,那么我们就说,这两个图形成中心对称;如果把一个图形绕着某一点旋转180度后能与自身重合,那么我们就说,这个图形成中心对称图形才能正确解答此题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目