题目内容
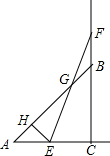 (2013•凤阳县模拟)如图,在△ABC中,∠ACB=90°,AC=BC=2.E、F分别是射线AC、CB上的动点,且AE=BF,EF与AB交于点G,EH⊥AB于点H,设AE=x,GH=y,下面能够反映y与x之间函数关系的图象是( )
(2013•凤阳县模拟)如图,在△ABC中,∠ACB=90°,AC=BC=2.E、F分别是射线AC、CB上的动点,且AE=BF,EF与AB交于点G,EH⊥AB于点H,设AE=x,GH=y,下面能够反映y与x之间函数关系的图象是( )分析:判断出△ABC是等腰直角三角形,然后再判断出△AHE是等腰直角三角形,根据等腰直角三角形的性质求出AB、AH的长,过点B作BD∥AC交EF于点D,然后利用平行线分线段成比例定理分别列式
=
,
=
,再表示出BD,然后求出BG的长度,最后根据GH=AB-AH-BG,代入数据整理即可得到y与x的函数关系式,再根据函数相应的图象解答.
| BD |
| AE |
| BG |
| AG |
| BF |
| FC |
| BD |
| EC |
解答: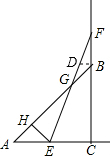 解:∵∠ACB=90°,AC=BC=2,
解:∵∠ACB=90°,AC=BC=2,
∴△ABC是等腰直角三角形,
∴AB=
=
=2
,∠A=45°,
∵EH⊥AB于点H,
∴△AHE是等腰直角三角形,
∴AH=
AE=
x,
过点B作BD∥AC交EF于点D,
则
=
,
=
,
∴BD=
•AE=
•x,BD=
•EC=
•(2-x),
∴
•x=
•(2-x),
整理得,BG(x+2)=(2
-BG)(2-x),
解得BG=
-
x,
根据图形,GH=AB-AH-BG,
=2
-
x-(
-
x),
=2
-
x-
+
x,
=
,
即y=
,是一条平行于x轴的直线.
故选C,
 解:∵∠ACB=90°,AC=BC=2,
解:∵∠ACB=90°,AC=BC=2,∴△ABC是等腰直角三角形,
∴AB=
| AC2+BC2 |
| 22+22 |
| 2 |
∵EH⊥AB于点H,
∴△AHE是等腰直角三角形,
∴AH=
| ||
| 2 |
| ||
| 2 |
过点B作BD∥AC交EF于点D,
则
| BD |
| AE |
| BG |
| AG |
| BF |
| FC |
| BD |
| EC |
∴BD=
| BG |
| AG |
| BG | ||
2
|
| BF |
| FC |
| x |
| x+2 |
∴
| BG | ||
2
|
| x |
| x+2 |
整理得,BG(x+2)=(2
| 2 |
解得BG=
| 2 |
| ||
| 2 |
根据图形,GH=AB-AH-BG,
=2
| 2 |
| ||
| 2 |
| 2 |
| ||
| 2 |
=2
| 2 |
| ||
| 2 |
| 2 |
| ||
| 2 |
=
| 2 |
即y=
| 2 |
故选C,
点评:本题考查了动点问题的函数图象,主要利用了等腰直角三角的判定与性质,平行线分线段成比例定理,作辅助线利用平行线分线段成比例定理两次表示出BD是解题的关键.

练习册系列答案
相关题目

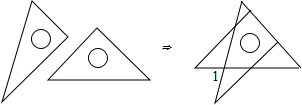 (2013•凤阳县模拟)将一副三角板如图叠放,问∠1的度数为( )
(2013•凤阳县模拟)将一副三角板如图叠放,问∠1的度数为( )